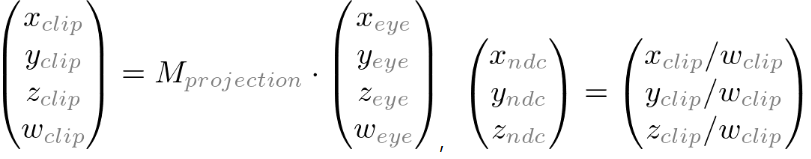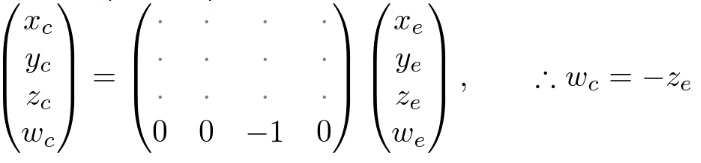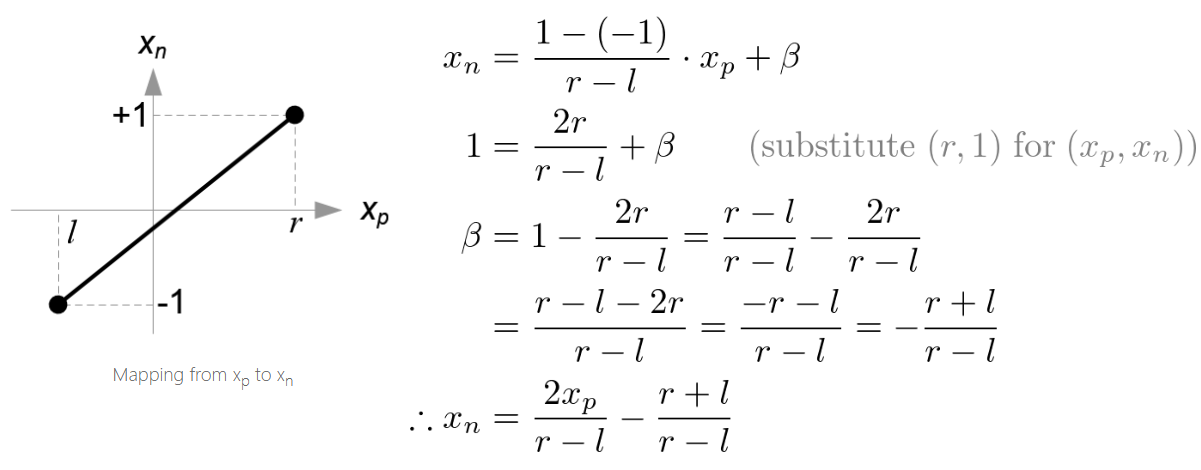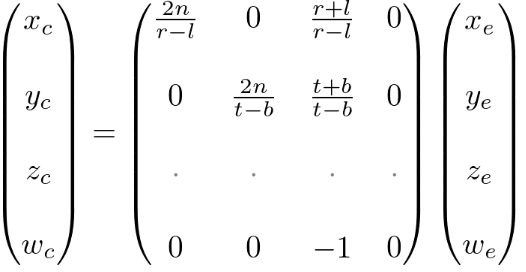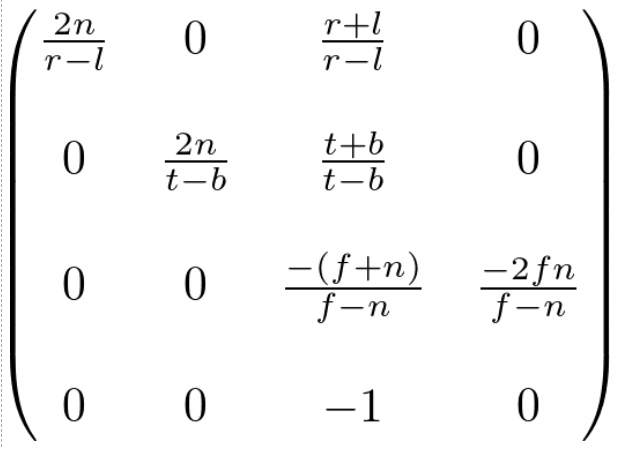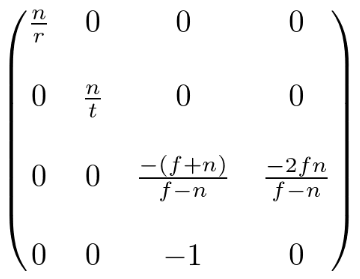投影矩阵详解

翻译自OpenGL Projection Matrix (songho.ca)

概览

电脑屏幕是一个二维平面，因此，由OpenGL渲染的三维场景需要作为一个2D图片被“投射”到电脑屏幕上。GL_PROJECTION矩阵是一个OpenGL内建的用于投影变换的矩阵。首先，它将所有顶点数据从观察空间变换到裁剪空间，随后，这些裁剪坐标经过齐次除法后被变换为NDC坐标。

因此，我们必须记住，GL_PROJECTION矩阵包含了两次变换：视锥体剔除以及NDC坐标变换。下面的章节讲述了如何利用left,right,bottom,top,near和far六个参数构建投影矩阵。

视锥体剔除发生于齐次除法之前。在剔除时，需要确定裁剪坐标$x_c$,$y_c$与$z_c$的范围。如果这三者在[$-w_c$, $w_c$]范围内，则保留，否则剔除。完成剔除后，OpenGL会重新构建多边形的边（通过增加顶点的方式）。

透视投影

在透视投影（Perspective Projection）中，位于平截头体（Truncated Pyramid Frustum）内部的顶点（观察空间下）会被映射到一个正立方体中。映射完毕后的三维坐标中，x分量从[l,r]映射到[-1,1]，y分量从[b,t]映射到[-1,1]，z分量从[-n,-f]映射到[-1,1]。

OpenGL中，观察空间是基于右手坐标系定义的，而NDC是基于左手坐标系的（直观表面为，垂直屏幕越往里，z分量越大），这意味着，在观察空间中，相机是看向-Z轴的（这意味着在观察空间中，near和far都是负值），而在NDC中相机是看向+Z轴的。

glFrustum()函数用于接收六个参数以构建平截头体。但参数中的near和far参数都必须为正，所以我们必须在构建投影矩阵的过程中把这两个参数取负值。

OpenGL中，观察空间下平截头体内部的顶点都将被投影到near平面上，该平面也被称为投影平面。下图展示了一个观察空间下的点是如何被投影到near平面上的：

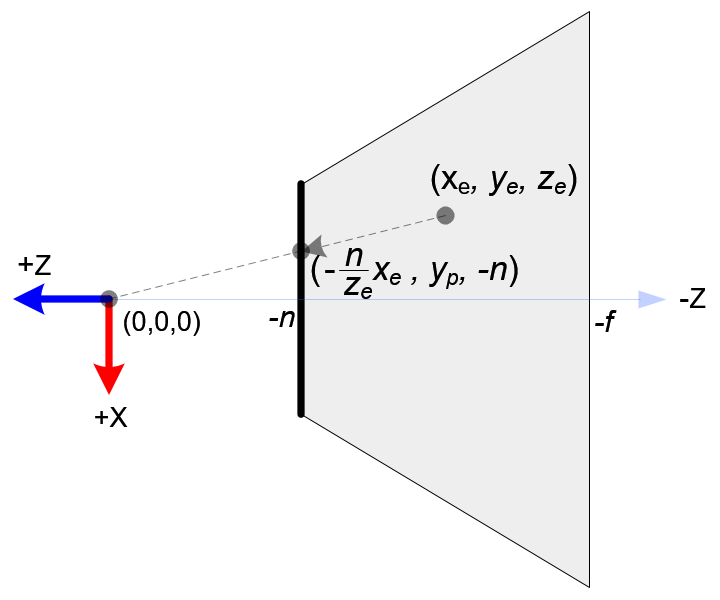
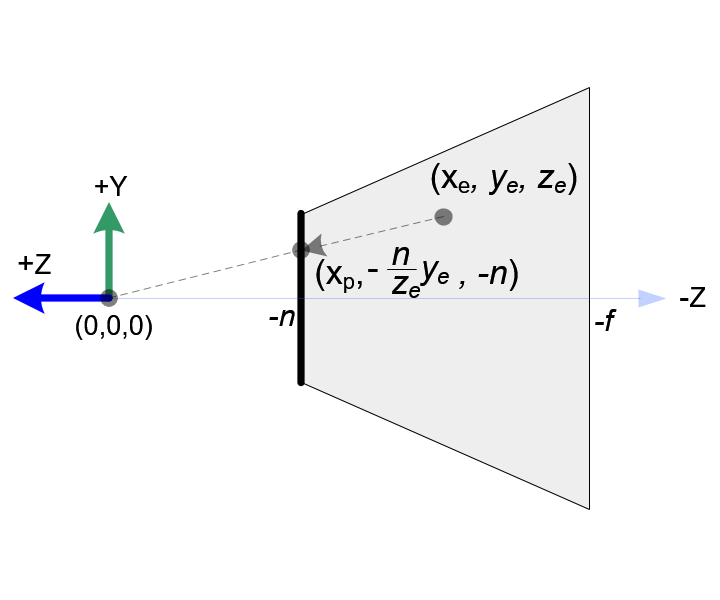
左图展示了平截头体的顶部视角，右图展示了平截头体的右侧视角。

从顶部视角，顶点的观察坐标的x分量从$x_e$映射到$x_p=\frac{n \cdot x_e}{-z_e}$。

从右侧视角，顶点的观察坐标y分量从$y_e$映射到$y_p = \frac{n \cdot y_e}{-z_e}$。

不难看出，$x_p$和$y_p$都与$z_e$相关，它们与$-z_e$成反比。也就是说，它们都除以了$-z_e$。

观察坐标通过GL_PROJECTION变换为裁剪坐标后，这个坐标仍然是一个齐次坐标（用n+1维表示的n维向量）。它最终通过将各分量除以w分量变换为NDC坐标。如图：

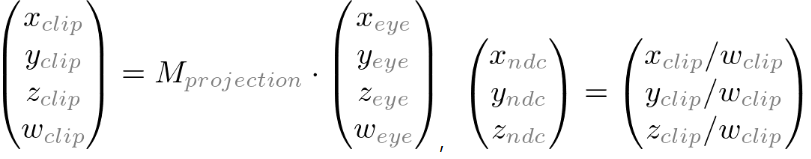
因此，$w_{c}$的值设置为$-z_e$。对于投影矩阵，它的第四行就应当是（0，0，-1，0）。如图：

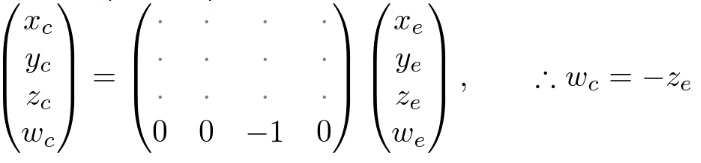
随后，我们把顶点投影坐标映射到NDC上，也就是：[l, r] ⇒ [-1, 1] and [b, t] ⇒ [-1, 1]

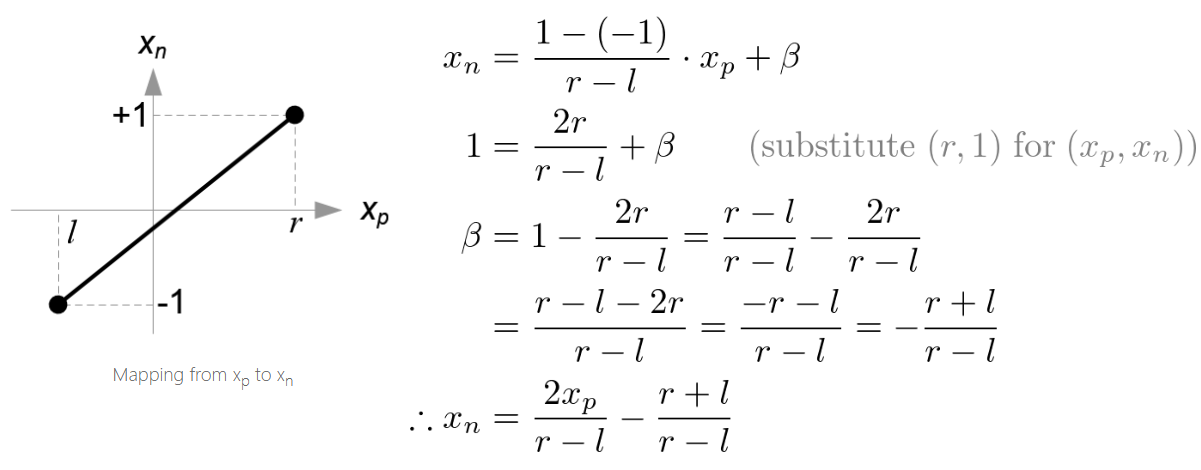
类似地，可以求得$y_n = \frac{2y_p}{t-b} - \frac{t+b}{t-b}$。

该如何理解映射过程？

我们知道，将法线贴图的RGB值（[0,1]）映射到[-1,1]时，我们采用的方法是*0.5+0.5。扩展一下，想要把[a,b]映射到[c,d]，所需要的公式如下：

$y = \frac{b-a}{d-c}\cdot x + α$ （称为公式①）

而当$x = b$时，$y = d$，代入公式①可得：

$d = \frac{b(b-a)}{d-c}+α$

解得$α = d - \frac{b(b-a)}{d-c}$

代入公式①即可得到映射函数：

$y = \frac{b-a}{d-c}\cdot x + \frac{b(b-a)}{d-c}$

得到$x_n$和$y_n$后，我们将$x_p$、$y_p$同$x_e$、$y_e$的关系式代入：

$x_n = \frac{2x_p}{r-l} - \frac{r+l}{r-l} = \frac{2\cdot \frac{n\cdot x_e}{-z_e}}{r-l} - \frac{r+l}{r-l} = (\frac{2n}{r-l}\cdot x_e+\frac{r+l}{r-l}\cdot z_e)/-z_e$

$y_n = \frac{2y_p}{t-b} - \frac{t+b}{t-b} = \frac{2\cdot \frac{n\cdot y_e}{-y_e}}{t-b} - \frac{t+b}{t-b} = (\frac{2n}{t-b}\cdot y_e+\frac{t+b}{t-b}\cdot z_e)/-z_e$

其中，最后结果中，括号内部的多项式分别代表裁剪坐标$x_c$和$y_c$。

根据这些线性方程组，我们可以推导出投影矩阵的前两行：

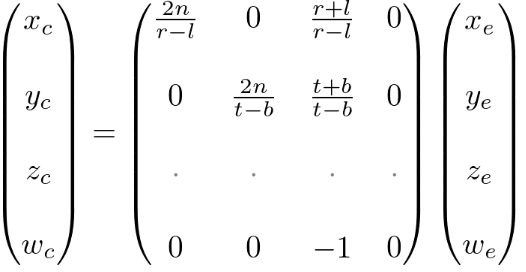
现在，我们求出投影矩阵的第三行就可以得到完整的投影矩阵了。

对于平截头体内的顶点，其观察空间下的z坐标在near平面下始终被投影至-near的值。但我们需要一个独特的z值用于裁剪和深度测试。此外，在一些后续处理中，我们有时会需要对裁剪坐标进行反变换，重新恢复到其他坐标。为了解决这一问题，我们对z分量做一些不同的处理：

首先我们知道，NDC坐标的z值$z_n$由裁剪坐标的z值$z_c$除以w值得到，即$z_n = z_c/w_c$。前面我们提到，$w_c=-z_e$，而z分量又是与x、y分量线性无关的，所以$z_c$只与$z_e$线性相关，可得：$z_c = Az_e+B$。代入得：

$z_n = \frac{Az_e+B}{-z_e} = -A-\frac{B}{z_e}$

已知$z_n$的范围是[-1,1]，$z_e$的范围是[-n,-f]，将上下限代入可得：

$\frac{-An+B}{n}=-1 ; \frac{Af+B}{f}=1$

联立解得$A = -\frac{f+n}{f-n} ，B=-\frac{2fn}{f-n}$

将A、B代入$Z_n$与A、B的线性方程，解得$Z_n = \frac{-\frac{f+n}{f-n}z_e-\frac{2fn}{f-n}}{-z_e}$

你可以注意到，Zn和Ze呈现非线性的关系。这意味着，在近平面附近，投影有着很高的精度，而在远平面处投影的精度就很低。当范围[-n,-f]覆盖的范围变大时，最终z值的精度就会丢失的越多（远平面附近物体z值的精细变化经过投影后可能失效）。因此，n和f应当尽可能缩小，以此来提高深度缓冲的精度。

由此可得完整的投影矩阵为：

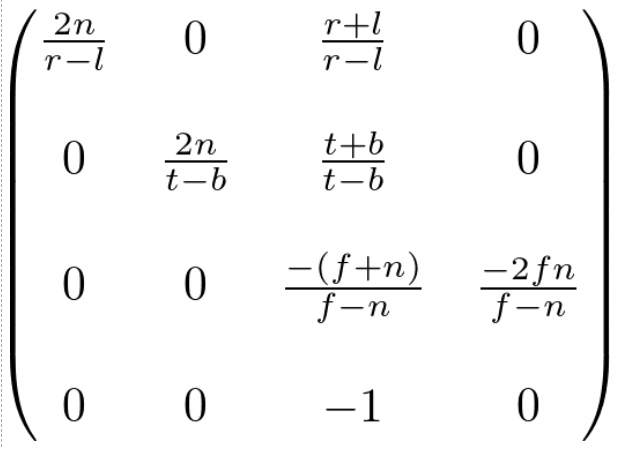
上面的矩阵适用于一般的平截头体。当视口对称时，则有$r=-l$，$t=-b$。此时投影矩阵可以简化为：

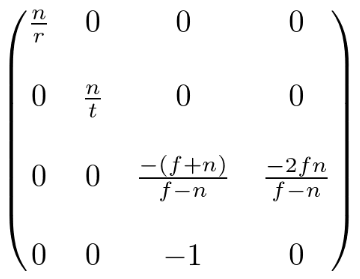
使用FOV的透视投影矩阵

给定near、far值和窗口大小时，很难确定top、bottom、left和right的值。但是我们可以从FOV的高宽比和窗口的宽高比推导出这四个参数。需要注意，高宽比和t,b,l,r之间的转换只能在对称透视投影矩阵的情况下进行。

当垂直FOV的值为θ，而屏幕宽高比未知时，我们可以通过直角三角形的特性计算出l,r,t,b四个参数。首先，使用1/2垂直FOV角度（θ/2）的正切构建公式①：

$tan(\frac{θ}{2})=t/n$

随后，借助屏幕宽高比计算屏幕宽度的一半，即r：

$r=t\cdot \frac{w}{h}$

踩坑

/**
 * 该函数输入一个投影相机的参数和一系列目标点的世界坐标，返回这些点在perspective投影面上的uv坐标以及深度值
 * 如果函数运行成功返回一个正数表示处理了多少个点，如果失败，返回0
 * xyz的单位不限，hpr的单位是弧度，UV取值在[0,1]时候才表示在视场内，不在视场内的点UV至少一个不在[0,1]之间，另外如果深度depth的返回值单位和xyz单位相同表示到相机的位置，对于不在视场内的点深度会统一赋值为-100.0;
 * @param camPos 相机绝对位置
 * @param camHpr 相机朝向 head pitch 和 roll，单位是弧度，注意角度弧度转换
 * @param camFovHoriz 相机水平的视场角，单位是弧度，注意角度弧度转换
 * @param camFovVerti 相机垂直的视场角，单位是弧度，注意角度弧度转换
 * @param tgtNum 需要计算的目标总数
 * @param tgtXYZs 目标世界坐标的数组
 * @param tgtUVDs 计算好的目标的uv坐标和深度
 * @return 成功返回处理了多少个点，失败返回0
 */
int TransProj(VM_D_XYZ camPos,VM_D_HPR camHpr,double camFovHoriz,double camFovVerti,int tgtNum,const VM_D_XYZ tgtXYZs[],VM_D_UVD tgtUVDs[]) {
    //------View矩阵计算------
    VM_D_XYZ camDir = GetDirectionFromHPR(camHpr);
    camDir.normalize();
    VM_D_MAT4 viewMat = LookAt(camPos,plus(camPos,camDir),vec3(0,0,1));
    //输出View矩阵
#ifdef DEBUG
    std::cout << "[DEBUG] ViewMat:" << std::endl;
    for(const auto & row : viewMat.rows) {
        std::cout << "[DEBUG] "<<row.to_string() << std::endl;
    }
#endif
    //------Proj矩阵计算------
    double near = 0.1;
    double far = 100.0f;
    double top = near * tan(camFovVerti/2);
    double right = near * tan(camFovHoriz/2);
    std::vector<VM_D_VEC4> rows;
    rows.push_back(vec4(near/right,0,0,0));
    rows.push_back(vec4(0,(far+near)/(far-near),0,-2*far*near/(far-near)));
    rows.push_back(vec4(0,0,near/top,0));
    rows.push_back(vec4(0,1 ,0,0));
    VM_D_MAT4 projMat = mat4(rows);
    //输出Proj矩阵
#ifdef DEBUG
    std::cout <<  "[DEBUG] "<<"ProjMat:" << std::endl;
    for(const auto & row : projMat.rows) {
        std::cout << "[DEBUG] "<< row.to_string() << std::endl;
    }
#endif
    int res = 0;
    //------坐标变换------
    for(int i=0;i<tgtNum;i++) {
        VM_D_VEC4 tgtVec = vec4(tgtXYZs[i],1.0);
        VM_D_VEC4 viewVec = Mul(viewMat,tgtVec);
        VM_D_MAT4 rollMat = GetRollMatrix(camHpr.r);
        viewVec = Mul(rollMat,viewVec);
        VM_D_VEC4 projVec = Mul(projMat,viewVec);
        VM_D_VEC4 NDCVec = vec4(projVec.x/projVec.w,projVec.y/projVec.w,projVec.z/projVec.w,1.0);
        VM_D_VEC4 UVVec = vec4((NDCVec.x+1)/2, (NDCVec.y+1)/2, (NDCVec.z+1)/2, 1.0);
        tgtUVDs[i].u = UVVec.x;
        tgtUVDs[i].v = UVVec.z;
        tgtUVDs[i].depth = viewVec.y; //sqrt(pow(tmpVec.x,2)+pow(tmpVec.y,2)+pow(tmpVec.z,2));
#ifdef DEBUG
        std::cout << "[DEBUG] "<< "------Transform Info: Point "<<i<<" ------" << std::endl;
        std::cout<< "[DEBUG] "<<"Target:"<<tgtXYZs[i].x<<","<<tgtXYZs[i].y<<","<<tgtXYZs[i].z<<std::endl;
        std::cout<< "[DEBUG] "<<"NDC Y component:"<<NDCVec.y<<std::endl;
        std::cout<< "[DEBUG] "<<"View Pos:"<<viewVec.x<<","<<viewVec.y<<","<<viewVec.z<<","<<viewVec.w<<std::endl;
        std::cout<< "[DEBUG] "<<"Projection Pos:"<<projVec.x<<","<<projVec.y<<","<<projVec.z<<","<<projVec.w<<std::endl;
#endif
#ifdef UVD
        std::cout<< "[UVDOutput] "<<"UV:"<<UVVec.x<<","<<UVVec.z<<std::endl;
#endif
        if(UVVec.x<0 || UVVec.x>1 || UVVec.z<0 || UVVec.z>1 || tgtUVDs[i].depth<=0) {
            tgtUVDs[i].depth = -100.0;
#ifdef DEBUG
            std::cout<< "[DEBUG] "<<"Out of View."<<std::endl;
#endif
        }
        else {
#ifdef DEBUG
            std::cout<< "[DEBUG] "<<"In View."<<std::endl;
#endif
        }
#ifdef UVD
        std::cout<< "[UVDOutput] "<<"Depth:"<<tgtUVDs[i].depth<<std::endl;
#endif
        res++;
    }
    return res;
}

/**
 * 根据相机位置、目标位置和世界坐标计算LookAt矩阵
 * @param cameraPos 相机位置
 * @param targetPos 目标位置
 * @param worldUp 世界坐标
 * @return LookAt矩阵
 */
VM_D_MAT4 LookAt(VM_D_XYZ cameraPos, VM_D_XYZ targetPos, VM_D_XYZ worldUp) {
    VM_D_XYZ cameraDir = minus(targetPos, cameraPos);
    cameraDir.normalize();
    VM_D_XYZ cameraRight = cross(cameraDir,worldUp);
    cameraRight.normalize();
    VM_D_XYZ cameraUp = cross( cameraRight,cameraDir);
    cameraUp.normalize();
    VM_D_MAT4 mat1 = mat4(1.0);
    mat1.rows[0] = vec4(cameraRight.x, cameraRight.y, cameraRight.z, 0.0);  // 相机坐标系的x轴正方向
    mat1.rows[1] = vec4(cameraDir.x, cameraDir.y, cameraDir.z, 0.0);        // 相机坐标系的y轴正方向
    mat1.rows[2] = vec4(cameraUp.x, cameraUp.y, cameraUp.z, 0.0);           // 相机坐标系的z轴正方向
    mat1.rows[3] = vec4(0.0, 0.0, 0.0, 1.0);
    VM_D_MAT4 mat2 = mat4(1.0);
    mat2.rows[0].w = -cameraPos.x;
    mat2.rows[1].w = -cameraPos.y;
    mat2.rows[2].w = -cameraPos.z;
    mat2.rows[3].w = 1.0f;
#ifdef DEBUG
    std::cout<<"[DEBUG] "<<"CameraRight:"<<cameraRight.x<<","<<cameraRight.y<<","<<cameraRight.z<<std::endl;
    std::cout<<"[DEBUG] "<<"CameraDir:"<<cameraDir.x<<","<<cameraDir.y<<","<<cameraDir.z<<std::endl;
    std::cout<<"[DEBUG] "<<"CameraUp:"<<cameraUp.x<<","<<cameraUp.y<<","<<cameraUp.z<<std::endl;
#endif
    return Mul(mat1, mat2);
}
/**
 * 根据HPR计算相机朝向方向
 * 注意：该函数默认Head为0时，方向向量指向x轴正方向。
 * @param hpc HPR，即head pitch 和 roll
 * @return 朝向方向
 */
VM_D_XYZ GetDirectionFromHPR(VM_D_HPR hpr) {
    VM_D_XYZ res;
    res.x = cos(hpr.h) * cos(hpr.p);
    res.z = sin(hpr.p); //z分量代表抬起角度
    res.y = -sin(hpr.h) * cos(hpr.p); //取反是因为本程序中y轴朝向正前方
#ifdef DEBUG
    std::cout<<"[DEBUG] "<<"DirectionFromHPR:"<<res.x<<","<<res.y<<","<<res.z<<std::endl;
#endif
    return res;
}
/**
 * 根据Roll角计算Roll变换矩阵
 * @param roll Roll角
 * @return Roll矩阵
 */
VM_D_MAT4 GetRollMatrix(double roll) {
    VM_D_MAT4 res = mat4(1.0);
    res.rows[0].x = cos(roll);
    res.rows[0].z = sin(roll);
    res.rows[2].x = -sin(roll);
    res.rows[2].z = cos(roll);
#ifdef DEBUG
    std::cout<<"[DEBUG] "<<"RollMatrix:"<<std::endl;
    for(const auto & row : res.rows) {
        std::cout<<"[DEBUG] "<<row.to_string()<<std::endl;
    }
#endif
    return res;
}

1. 教程所给的投影矩阵，默认正y轴为世界空间上向量，并且深度越大，z轴越小。
2. LookAt矩阵中，相机的朝向、上轴和右轴指的是相机本身的坐标系。例如，相机默认朝向正Y轴时，矩阵的第二行就应当是相机朝向向量的三个分量。