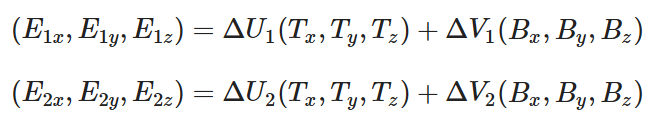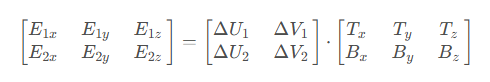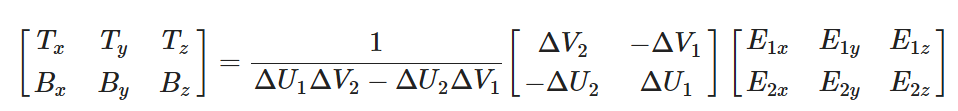LearnOpenGL学习笔记（十二） - 万向阴影贴图、法线贴图与视差贴图

本文最后更新于 2024年8月24日晚上

快速过一遍。

点光源阴影

对于平行光，我们只需要考虑一个方向。但点光源就需要考虑所有方向了。Cube Map这时候就派上用场了。

我们以点光源为原点，以90的FOV对六个方向进行深度图渲染，然后将其拼接为CubeMap，供方向向量采样。具体如下：

首先，创建立方体贴图，绑定至目标GL_TEXTURE_CUBE_MAP，然后创建六个数据值为NULL的2D纹理，映射到CubeMap的六个面上：

GLuint depthCubemap;
glGenTextures(1, &depthCubemap);
const GLuint SHADOW_WIDTH = 1024, SHADOW_HEIGHT = 1024;
glBindTexture(GL_TEXTURE_CUBE_MAP, depthCubemap);
for (GLuint i = 0; i < 6; ++i)
        glTexImage2D(GL_TEXTURE_CUBE_MAP_POSITIVE_X + i, 0, GL_DEPTH_COMPONENT, 
                     SHADOW_WIDTH, SHADOW_HEIGHT, 0, GL_DEPTH_COMPONENT, GL_FLOAT, NULL);
glTexParameteri(GL_TEXTURE_CUBE_MAP, GL_TEXTURE_MAG_FILTER, GL_NEAREST);
glTexParameteri(GL_TEXTURE_CUBE_MAP, GL_TEXTURE_MIN_FILTER, GL_NEAREST);
glTexParameteri(GL_TEXTURE_CUBE_MAP, GL_TEXTURE_WRAP_S, GL_CLAMP_TO_EDGE);
glTexParameteri(GL_TEXTURE_CUBE_MAP, GL_TEXTURE_WRAP_T, GL_CLAMP_TO_EDGE);
//注意CubeMap的R分量也要设置环绕方式
glTexParameteri(GL_TEXTURE_CUBE_MAP, GL_TEXTURE_WRAP_R, GL_CLAMP_TO_EDGE);

接着，绑定光空间渲染帧缓冲，并将CubeMap作为帧缓冲的纹理附件，类型为GL_DEPTH_ATTACHMENT：

glBindFramebuffer(GL_FRAMEBUFFER, depthMapFBO);
glFramebufferTexture(GL_FRAMEBUFFER, GL_DEPTH_ATTACHMENT, depthCubemap, 0);
// 当不需要颜色缓冲时，就调用下面两行
glDrawBuffer(GL_NONE);
glReadBuffer(GL_NONE);
glBindFramebuffer(GL_FRAMEBUFFER, 0);

随后，进行光空间变换。由于CubeMap存在六个面，所以需要创建六个观察矩阵：

GLfloat aspect = (GLfloat)SHADOW_WIDTH/(GLfloat)SHADOW_HEIGHT;
GLfloat near = 1.0f;
GLfloat far = 25.0f;
glm::mat4 shadowProj = glm::perspective(glm::radians(90.0f), aspect, near, far);
std::vector<glm::mat4> shadowTransforms;
shadowTransforms.push_back(shadowProj * 
                 glm::lookAt(lightPos, lightPos + glm::vec3(1.0,0.0,0.0), glm::vec3(0.0,-1.0,0.0)));
shadowTransforms.push_back(shadowProj * 
                 glm::lookAt(lightPos, lightPos + glm::vec3(-1.0,0.0,0.0), glm::vec3(0.0,-1.0,0.0)));
shadowTransforms.push_back(shadowProj * 
                 glm::lookAt(lightPos, lightPos + glm::vec3(0.0,1.0,0.0), glm::vec3(0.0,0.0,1.0)));
shadowTransforms.push_back(shadowProj * 
                 glm::lookAt(lightPos, lightPos + glm::vec3(0.0,-1.0,0.0), glm::vec3(0.0,0.0,-1.0)));
shadowTransforms.push_back(shadowProj * 
                 glm::lookAt(lightPos, lightPos + glm::vec3(0.0,0.0,1.0), glm::vec3(0.0,-1.0,0.0)));
shadowTransforms.push_back(shadowProj * 
                 glm::lookAt(lightPos, lightPos + glm::vec3(0.0,0.0,-1.0), glm::vec3(0.0,-1.0,0.0)));

然后，把shadowTransforms中的六个变换矩阵发送到着色器。

在这里，我们需要使用几何着色器，将原来的三角形图元变换到六个坐标系下，并分别在这些坐标系下生成新的图元，供片段着色器使用。

对于顶点着色器，由于坐标变换在几何着色器中完成，所以只需要进行世界坐标变换即可。

#version 330 core
layout (location = 0) in vec3 position;
uniform mat4 model;
void main()
{
    gl_Position = model * vec4(position, 1.0);
}

几何着色器接收六元素的光坐标变换矩阵数组，对gl_Position进行坐标变换，然后发射顶点。

为什么要经过几何着色器，而非直接在片段着色器进行六次变换？

在片段着色器中处理六个不同的光变换矩阵会导致冗余计算，因为每个片段都需要判断其应属于哪个方向的阴影贴图。而几何着色器可以一次处理六个光方向变换，减少了片段着色器的调用次数，减少了性能开销。

但在某些显卡驱动上，几何着色器速度比较慢。所以得看具体情况。

#version 330 core
layout (triangles) in;
layout (triangle_strip, max_vertices=18) out; //共计6*3=18个顶点
uniform mat4 shadowMatrices[6];
out vec4 FragPos;
void main(){
    for(int face = 0; face < 6; ++face){
        //gl_Layer指定了发送图元到CubeMap的哪个面
        gl_Layer = face;
        for(int i = 0; i < 3; ++i){
            FragPos = gl_in[i].gl_Position;
            gl_Position = shadowMatrices[face] * FragPos;
            EmitVertex();
        }    
        EndPrimitive();
    }
}

这一步是如何运作的？

我们想象一下，一个固定视角的摄像机。六个变换，都会把各自方向上应当渲染的物体变换到摄像机正前方。六次变换完毕后，相当于六个场景的物体都挤在一起，叠加在正前方。六个场景的物体都有一个Tag（gl_Layer，指定了当前图元在CubeMap中处于的面)，每次只渲染其中的一个Tag到CubeMap上，直到六个面都渲染完为止。

接下来我们手动配置片段深度，在片段着色器中完成：

#version 330 core
in vec4 FragPos;
uniform vec3 lightPos;
uniform float far_plane;
void main(){
    // get distance between fragment and light source
    float lightDistance = length(FragPos.xyz - lightPos);
    // map to [0;1] range by dividing by far_plane
    lightDistance = lightDistance / far_plane;
    // write this as modified depth
    gl_FragDepth = lightDistance;
}

随后，CubeMap深度贴图生成完毕，进入渲染阶段。

与2D纹理深度贴图类似，使用glActiveTexture和glBindTexture绑定CubeMap材质。

然后，修改顶点着色器，使其按照类似于无阴影时的方式，用MVP矩阵变换顶点坐标并传给片段着色器：gl_Position = projection * view * model * vec4(position, 1.0f);

对于片段着色器，将原本depthMap uniform的类型变更为samplerCube，并用FragPos作为采样向量即可。

新的阴影计算函数：

float ShadowCalculation(vec3 fragPos){
    vec3 fragToLight = fragPos - lightPos;
    //对CubeMap采样的方向向量无需归一化
    float closestDepth = texture(depthMap, fragToLight).r;
    //变换深度值从[0,1]到[0,far_plane]
    closestDepth *= far_plane;
    //手动计算当前深度值，即片段到光源的距离
    float currentDepth = length(fragToLight);
    float bias = 0.05; 
    float shadow = currentDepth -  bias > closestDepth ? 1.0 : 0.0;
    return shadow;
}

踩坑

传递给几何着色器的光变换矩阵的投影矩阵的近平面不能过大，最好<0.5f。
CalculateShadow()函数的返回值应当One Minus后再乘以各光照分量。
光空间帧缓冲渲染所用的顶点着色器只需要对传入的顶点位置做世界空间变换。
渲染光空间帧缓冲时，需要调整glViewPort至阴影贴图的分辨率。

PCF

与单阴影贴图类似，万向阴影贴图同样存在由于贴图分辨率导致的阴影走样问题。可以使用PCF技术，对周围像素采样、平均，减少走样程度：

float shadow = 0.0;
float bias = 0.05; 
float samples = 4.0; //每个维度的采样次数
float offset = 0.1;
for(float x = -offset; x < offset; x += offset / (samples * 0.5)){
    for(float y = -offset; y < offset; y += offset / (samples * 0.5)){
        for(float z = -offset; z < offset; z += offset / (samples * 0.5)){
            float closestDepth = texture(depthMap, fragToLight + vec3(x, y, z)).r; 
            closestDepth *= far_plane;   // Undo mapping [0;1]
            if(currentDepth - bias > closestDepth)
                shadow += 1.0;
        }
    }
}
shadow /= (samples * samples * samples);

然而，上面的代码对每个片段都需要采样4*4*4=64次，性能开销大。我们需要抛弃一些彼此距离非常近的采样点，转而使用彼此分的比较开的采样点。为此，我们设定一个采样方向数组，里面包含了若干个vec3，彼此分离的很开，并且指向不同的方向。

vec3 sampleOffsetDirections[20] = vec3[]
(
   vec3( 1,  1,  1), vec3( 1, -1,  1), vec3(-1, -1,  1), vec3(-1,  1,  1), 
   vec3( 1,  1, -1), vec3( 1, -1, -1), vec3(-1, -1, -1), vec3(-1,  1, -1),
   vec3( 1,  1,  0), vec3( 1, -1,  0), vec3(-1, -1,  0), vec3(-1,  1,  0),
   vec3( 1,  0,  1), vec3(-1,  0,  1), vec3( 1,  0, -1), vec3(-1,  0, -1),
   vec3( 0,  1,  1), vec3( 0, -1,  1), vec3( 0, -1, -1), vec3( 0,  1, -1)
);
float shadow = 0.0;
float bias = 0.15;
int samples = 20;
float viewDistance = length(viewPos - fragPos);
//此处diskRadius就是offset
//这里采样的技巧是，当观察者距离片段越远，阴影越柔和，否则越锐利
float diskRadius = (1.0 + (viewDistance / far_plane)) / 25.0; 
for(int i = 0; i < samples; ++i)
{
    float closestDepth = texture(depthMap, fragToLight + sampleOffsetDirections[i] * diskRadius).r;
    closestDepth *= far_plane;   // Undo mapping [0;1]
    if(currentDepth - bias > closestDepth)
        shadow += 1.0;
}
shadow /= float(samples);

法线贴图

法线贴图（Normal Map）用于对顶点的法线作手动偏移。

类似于漫反射和镜面贴图，法线贴图是一个2D纹理，它的每个像素的颜色是一个vec3（颜色的r、g、b值，刚好是三个分量），代表着使用此处纹理坐标采样的片段的法线。

法线向量的范围在[-1,1]，而RGB颜色的值在[0,1]，所以要先进行处理：

1
2
3

vec3 rgb_normal = normal * 0.5 + 0.5; // 从法线向量转换为颜色向量
// 或
vec3 normal = (rgb_normal - 0.5) / 0.5 //从颜色向量转换为法线向量

法线贴图看起来是这样的：

一般法线贴图都偏向蓝色，因为正对“屏幕外”的法线指向(0,0,1)，即Z轴，这是一种偏向蓝色的颜色。对于偏“上方”的法线，指向Y轴(0,1,0)，就偏绿。

但是，要想让复杂模型正确应用法线贴图，就需要把采样得到的法线值进行坐标变换。

法线贴图中存储的法线向量处于切线空间（Tangent Space）。在切线空间中，法线永远指向正Z方向。

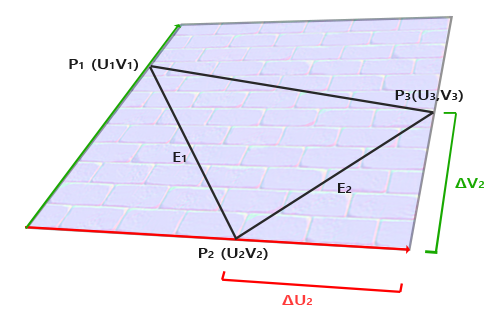
将切线空间的Z方向和顶点法线方向对齐的变换矩阵叫做TBN矩阵（Tangent、Bitangent、Normal）。顾名思义，构建此矩阵需要三个向量：法线向量N、切线向量T、副切线向量B。

法线向量可以直接从顶点属性中获取。其余两个向量需要计算获得。

如图，三角形边E1、E2可以被看做是切线向量T和副切线向量B的线性组合：

转换为矩阵乘法：

变换（乘逆矩阵）可得：

由此，可计算出T和B。

代码形式如下：

// positions
glm::vec3 pos1(-1.0,  1.0, 0.0);
glm::vec3 pos2(-1.0, -1.0, 0.0);
glm::vec3 pos3(1.0, -1.0, 0.0);
glm::vec3 pos4(1.0, 1.0, 0.0);
// texture coordinates
glm::vec2 uv1(0.0, 1.0);
glm::vec2 uv2(0.0, 0.0);
glm::vec2 uv3(1.0, 0.0);
glm::vec2 uv4(1.0, 1.0);
// normal vector
glm::vec3 nm(0.0, 0.0, 1.0);
glm::vec3 edge1 = pos2 - pos1; //E1
glm::vec3 edge2 = pos3 - pos1; //E2
glm::vec2 deltaUV1 = uv2 - uv1; //ΔU
glm::vec2 deltaUV2 = uv3 - uv1; //ΔV
GLfloat f = 1.0f / (deltaUV1.x * deltaUV2.y - deltaUV2.x * deltaUV1.y);
//计算三角形1的切线与副切线
tangent1.x = f * (deltaUV2.y * edge1.x - deltaUV1.y * edge2.x);
tangent1.y = f * (deltaUV2.y * edge1.y - deltaUV1.y * edge2.y);
tangent1.z = f * (deltaUV2.y * edge1.z - deltaUV1.y * edge2.z);
tangent1 = glm::normalize(tangent1);
bitangent1.x = f * (-deltaUV2.x * edge1.x + deltaUV1.x * edge2.x);
bitangent1.y = f * (-deltaUV2.x * edge1.y + deltaUV1.x * edge2.y);
bitangent1.z = f * (-deltaUV2.x * edge1.z + deltaUV1.x * edge2.z);
bitangent1 = glm::normalize(bitangent1);  

[...] // 对平面的第二个三角形采用类似步骤计算切线和副切线

我们把计算得到的切线、副切线向量作为顶点属性传递给顶点着色器，供顶点着色器构造TBN矩阵：

#version 330 core
layout (location = 0) in vec3 position;
layout (location = 1) in vec3 normal;
layout (location = 2) in vec2 texCoords;
layout (location = 3) in vec3 tangent;
layout (location = 4) in vec3 bitangent; //实际上，副切线向量可以用cross(T,N)得到，无需传递
void main()
{
   [...]
   vec3 T = normalize(vec3(model * vec4(tangent,   0.0)));
   vec3 B = normalize(vec3(model * vec4(bitangent, 0.0)));
   vec3 N = normalize(vec3(model * vec4(normal,    0.0)));
   mat3 TBN = mat3(T, B, N)
   [...]
}

一种方式是将TBN矩阵传递至片段着色器，将采样得到的法线乘以TBN矩阵，将其从切线空间变换到世界空间。但这种方式在片段着色器中引入了矩阵乘法，增加了许多性能开销。

第二种方式是在顶点着色器中，首先获取TBN矩阵的逆矩阵（由于TBN正交，所以获取其transpose矩阵即可），然后用这个逆矩阵把光照方向、观察方向等相关向量变换到切线空间，再传递给片段着色器。

out VS_OUT {
    vec3 FragPos;
    vec2 TexCoords;
    vec3 TangentLightPos;
    vec3 TangentViewPos;
    vec3 TangentFragPos;
} vs_out;
uniform vec3 lightPos;
uniform vec3 viewPos;
[...]
void main()
{    
    [...]
    mat3 TBN = transpose(mat3(T, B, N));
    vs_out.TangentLightPos = TBN * lightPos;
    vs_out.TangentViewPos  = TBN * viewPos;
    vs_out.TangentFragPos  = TBN * vec3(model * vec4(position, 0.0));
    [...]
}

Assimpt API

使用Assimp的importer进行模型导入时，使用aiProcess_CalcTangentSpace的Flag，即可自动为每个顶点计算切线与副切线向量，并使用aiMesh类的mTangents[i]获取切线向量，使用mBitangents[i]获取副切线向量。

1
2
3

const aiScene* scene = importer.ReadFile(
    path, aiProcess_Triangulate | aiProcess_FlipUVs | aiProcess_CalcTangentSpace
);

Assimp无法使用aiTextureType_NORMAL加载.obj的法线贴图，而是得使用aiTextureType_HEIGHT。

施密特正交化

当法线贴图应用到高面数模型时，通过类似于采样周边像素的方式对法线进行平均化能获得较平滑的结果。但是，这会导致TBN矩阵并非正交矩阵。

可以使用施密特正交化让TBN向量重新相互正交。

vec3 T = normalize(vec3(model * vec4(tangent, 0.0)));
vec3 N = normalize(vec3(model * vec4(normal, 0.0)));
// re-orthogonalize T with respect to N
T = normalize(T - dot(T, N) * N);
// then retrieve perpendicular vector B with the cross product of T and N
vec3 B = cross(T, N);
mat3 TBN = mat3(T, B, N)

视差贴图

法线贴图只是对光照的欺骗操作，而视差贴图（Paralax Mapping）则让平面贴图真正“拥有”深度。

视差贴图与光照无关，它根据存储在纹理中的几何信息对顶点进行偏移。

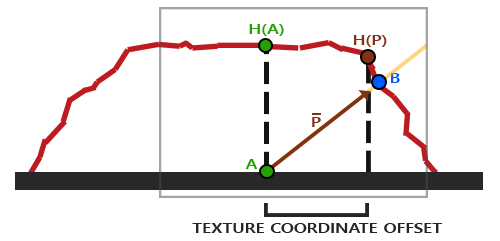
然而，一个平面基本不会有那么多顶点用于偏移。实际上，视差贴图是通过修改纹理坐标来让片段看起来比实际的更高或者更低的。如图：

红线代表视差贴图中的数值，V代表ViewDir，A代表片段位置。视差贴图的目的是，渲染片段A时，不再使用A处的纹理坐标，而是使用B处的。实现方式如下：

采样视差贴图的A处，可以得到H(A)，代表着对viewDir向量（原V向量）进行缩放后的长度。缩放后得到向量P。

随后，得到向量P在视差贴图上的投影，取其长度作为纹理坐标偏移值。

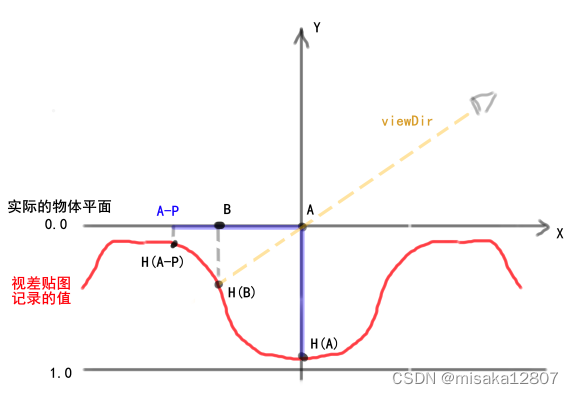
为什么这个能work？

对于现实中的物体，我们看向A处时，实际上只会看到B。我们通过这种方法偏移纹理坐标，最终采样的位置十分接近B。H(P)点与B越接近，效果越接近现实。

但是，我们在视差贴图的采样过程中引入了另一个坐标空间，在这个空间中，P向量的x、y分量总是与贴图表面对齐。当表面被旋转后，由于坐标空间未变化，我们会得到错误的结果。

为了解决这一问题，视差贴图往往是在切线空间实现的。我们要做的就是把V向量转换到切线空间。

实现

视差贴图需要与法线贴图结合使用，因为如果光照与视差效果不匹配，就很出戏了。

一般情况下，我们用“深度”图而非“高度”图作为视差贴图。如下：

视差贴图示意

vec2 ParallaxMapping(vec2 texCoords, vec3 viewDir)
{ 
    float height =  texture(depthMap, texCoords).r;    
    vec2 p = viewDir.xy / viewDir.z * (height * height_scale);
    return texCoords - p;    
}

上面是一种相对简单的视差函数实现。其中，viewDir.xy / viewDir.z求取的是viewDir在z轴方向的“倾斜度”。当viewDir与纹理表面越平行，获取的偏移向量p就越大。这个函数返回偏移以后的纹理坐标，我们使用这个纹理坐标采样漫反射贴图。

陡峭视差映射

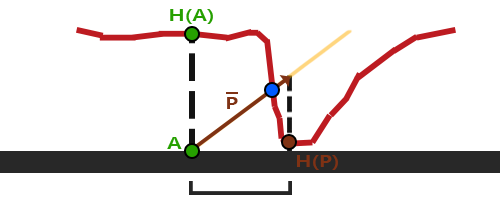
在表面高度变化较大的情况下，会出现一些不好的结果。原理图如下：

当蓝点与H(P)点距离越大时，画面表现就越不真实。为解决这一问题，我们引入陡峭视差映射（Steep Parallax Mapping）技术：

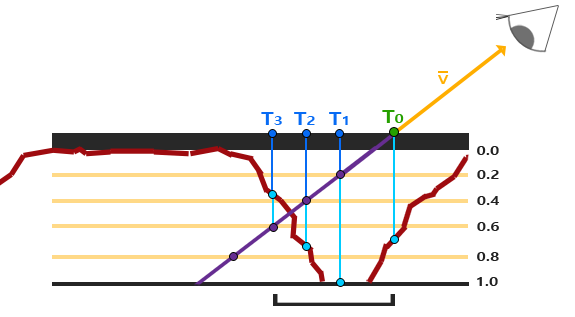
SPM技术的基本思想是，把总深度范围划分为若干层，每采样一次，便移动纹理坐标，并下降一层继续采样，直到采样深度小于当前层的深度值为止。

vec2 ParallaxMapping(vec2 texCoords, vec3 viewDir)
{ 
    const float minLayers = 8;
    const float maxLayers = 32;
    float numLayers = mix(maxLayers, minLayers, abs(dot(vec3(0.0, 0.0, 1.0), viewDir)));
    float layerDepth = 1.0 / numLayers;
    float currentLayerDepth = 0.0;
    vec2 P = viewDir.xy * height_scale; 
    vec2 deltaTexCoords = P / numLayers;
	vec2  currentTexCoords     = texCoords;
	float currentDepthMapValue = texture(depthMap, currentTexCoords).r;
	while(currentLayerDepth < currentDepthMapValue)
	{
        currentTexCoords -= deltaTexCoords;
        currentDepthMapValue = texture(depthMap, currentTexCoords).r;  
        currentLayerDepth += layerDepth;  
	}
	return currentTexCoords;
}

视差遮蔽映射

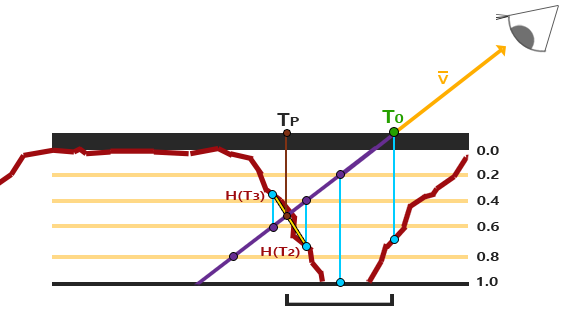
视差遮蔽映射（Parallax Occlusion Mapping）用于减少陡峭视差映射的断层现象。其原理与陡峭视差映射相同，但并非使用第一次纹理采样值大于采样层深度的采样层深度作为纹理坐标偏移量，而是：当满足条件时，使用当前层的深度和上一层深度的比例关系作为插值权重，对当前层对应的纹理坐标和上一层对应的纹理坐标进行插值。如图：

代码如下：

[...]
vec2 prevTexCoords = currentTexCoords + deltaTexCoords;
float afterDepth  = currentDepthMapValue - currentLayerDepth;
float beforeDepth = texture(depthMap, prevTexCoords).r - currentLayerDepth + layerDepth;
float weight = afterDepth / (afterDepth - beforeDepth);
vec2 finalTexCoords = prevTexCoords * weight + currentTexCoords * (1.0 - weight);
return finalTexCoords;

#图形学 #OpenGL #学习笔记

LearnOpenGL学习笔记（十二） - 万向阴影贴图、法线贴图与视差贴图

http://example.com/2024/08/24/LearnOpenGL学习笔记（十二）-万向阴影贴图、法线贴图与视差贴图/

作者

Yoi

发布于

2024年8月24日

许可协议

LearnOpenGL学习笔记（十三） - HDR、泛光、延迟渲染与SSAO 上一篇

投影矩阵详解下一篇