GAMES101学习笔记（一） - 变换、光栅化与几何

漫漫长路。

变换

基本变换

缩放

\symbf{S}(s_x,s_y,s_z) = $\begin{bmatrix}s_x&0&0&0\\0&s_y&0&0\\0&0&s_y&0\\0&0&0&1\end{bmatrix}$

其中，$s_i$为轴$i$方向上的缩放倍数。

当缩放倍数为负数时，相当于在对应的轴上做了翻转。

切变

切变（Shear）操作可以改变物体的形状。

$\begin{bmatrix}x'\\y'\end{bmatrix}$ = $\begin{bmatrix}1&a\\0&1\end{bmatrix}$ $\begin{bmatrix}x\\y\end{bmatrix}$

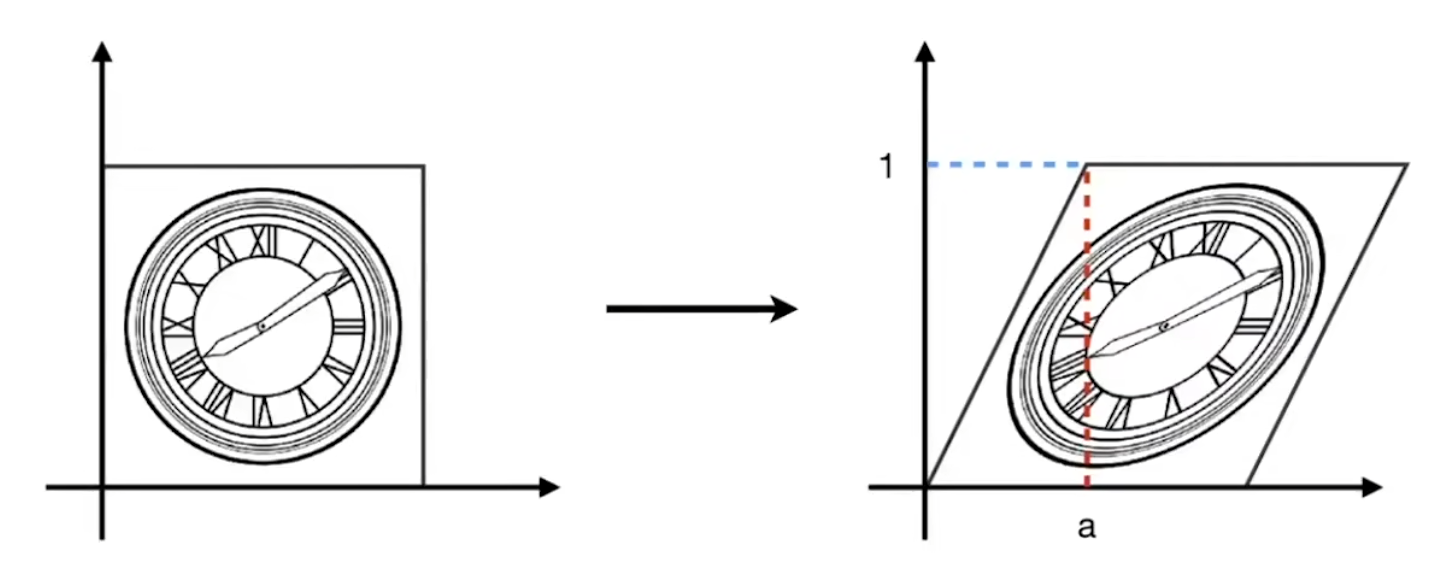
旋转

对于二维物体，绕原点逆时针旋转$\theta$度：

$\begin{bmatrix}x'\\y’\end{bmatrix}$ = $\begin{bmatrix}cos\theta &-sin \theta\\sin\theta&-cos\theta\end{bmatrix}$ $\begin{bmatrix}x\\y\end{bmatrix}$

如果想绕任意一个点旋转，可以将该变换分解为三步：

1. 平移到原点
2. 绕原点旋转
3. 平移到原来的位置

相反地，顺时针旋转$\theta$度等价于逆时针旋转$-\theta$度，其变换矩阵为：

$\begin{bmatrix}x’\\y’\end{bmatrix}$ = $\begin{bmatrix}cos\theta&sin\theta\\-sin\theta&-cos\theta\end{bmatrix}$$\begin{bmatrix}x\\y\end{bmatrix}$

可以看出，反方向的旋转变换矩阵等于正方向变换矩阵的转置，即$R_{-\theta} = {R_{\theta}}^T$。

同时，根据定义，正方向旋转变换矩阵的逆矩阵就是反方向旋转变换矩阵。由此可以推出，对于旋转变换矩阵，其转置矩阵与逆矩阵相同，因此旋转变换矩阵是正交矩阵。

对于三维空间：

\symbf{R}_x(\alpha) = \begin{bmatrix}1&0&0&0\\0&cos\alpha&-sin\alpha&0\\0&sin\alpha&cos\alpha&0\\0&0&0&1\end{bmatrix}

\symbf{R}_y(\alpha) = \begin{bmatrix}cos\alpha&0&sin\alpha&0\\0&1&0&0\\-sin\alpha&0&cos\alpha&0\\0&0&0&1\end{bmatrix}

\symbf{R}_z(\alpha) = \begin{bmatrix}cos\alpha&-sin\alpha&0&0\\sin\alpha&cos\alpha&0&0\\0&0&1&0\\0&0&0&1\end{bmatrix}

简记：绕哪轴，哪不变，xz应用2D矩阵，y2D转置。

由于在右手坐标系中，y轴正方向由z叉乘x得到，因此符号相反。

欧拉角：\symbf{R}_{xyz}(\alpha,\beta,\gamma) = \symbf{R}_x(\alpha)\ \symbf{R}_y(\beta)\ \symbf{R}_z(\gamma)

罗德里格斯旋转公式（Rodrigues’ Rotation Formula）：给定一个角度$\alpha$和一个轴$n$，得到变换矩阵：

\symbf{R}(\symbf{n},\alpha) = cos(\alpha)\symbf{I} + (1-cos(\alpha))\symbf{nn}^T + sin(\alpha) \begin{bmatrix}0&-n_z&n_y\\n_z&0&-n_x\\-n_y&n_x&0\end{bmatrix}

其中，I是单位矩阵；sin(α)后的矩阵实际上是向量n的叉乘矩阵表示。

该公式默认轴n过原点。若要绕任意轴旋转，可以先将目标点平移到原点，然后用此公式生成变换矩阵。

平移

\symbf{T}(t_x,t_y,t_z) = $\begin{bmatrix}1&0&0&t_x\\0&1&0&t_y\\0&0&1&t_z\\0&0&0&1\end{bmatrix}$

齐次坐标

齐次坐标（Homogeneous Coordinates）用于实现平移变换。

齐次坐标会给n维的点或向量增加一个维度$w$，用于实现平移变换。其中，点的$w$分量固定为1，而向量的$w$分量固定为0（因为向量平移没有意义）。以二维坐标为例：

$\begin{bmatrix}x'\\y'\\w'\end{bmatrix}$ = $\begin{bmatrix}1&0&t_x\\0&1&t_y\\0&0&1\end{bmatrix} ·$$\begin{bmatrix}x\\y\\z\end{bmatrix}$ = $\begin{bmatrix}x+t_X\\y+t_y\\1\end{bmatrix}$

$w$分量要么是0，要么是1，分别代表着向量和点。这一性质在向量和点之间的加减运算后仍然保留，例如向量+向量=向量（0+0=0），向量+点=点（0+1=1）等。

对于大于1的$w$分量，我们引入定义：

在齐次坐标系中，$\begin{bmatrix}x\\y\\x\\w\end{bmatrix}$代表点$\begin{bmatrix}x/w\\y/w\\z/w\\1\end{bmatrix}$，其中$w$≠0。

在没有齐次坐标的情况下，我们可以用下面的表达式表示平移：

$\begin{bmatrix}x’\\y’\end{bmatrix}$ = $\begin{bmatrix}a&b\\c&d\end{bmatrix}$·$\begin{bmatrix}x\\y\end{bmatrix}$+$\begin{bmatrix}t_x\\t_y\end{bmatrix}$

该变换称为仿射变换（Affine Transformations）。

所有仿射变换都可以表示为齐次坐标。

逆变换

逆变换矩阵就是原变换矩阵的逆矩阵。

变换组合

由于矩阵没有交换律，所以变换矩阵的顺序十分重要。

存在多个矩阵同时与向量相乘时，先应用的是最靠近向量的变换矩阵，以此类推。

组合的顺序为：先缩放，再旋转，最后平移。

观测变换

观测变换（Viewing Transformation）包含了视图变换（View Transformation）和投影变换（Projection Transformation)。

视图变换

首先确定定义相机所需的参数：

• 位置$\vec{e}$
• 朝向向量$\hat{g}$
• 上方向$\hat{t}$ （影响相机本身在世界空间内的旋转）

我们约定，根据相对关系，相机永远处于原点，面向Z轴负方向，以Y轴正方向为上方向。视图变换所做的是让其他物体移动，而非让相机移动。

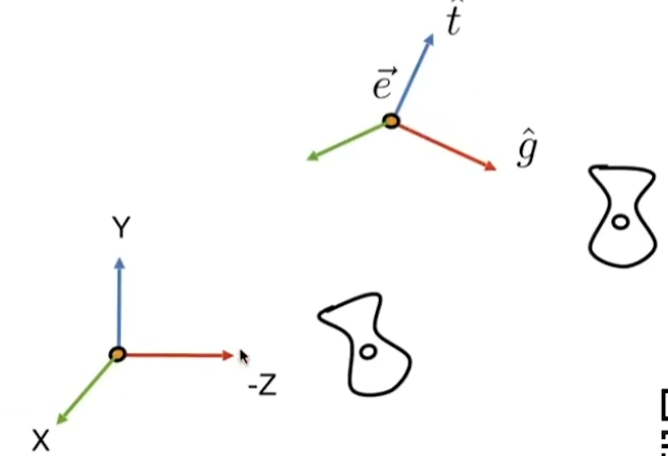
我们可以将视图变换矩阵$M_{view}$拆解为下面几个变化：

1. 将位置$\vec{e}$变换到原点：
2. 旋转朝向向量$\hat{g}$到z轴负方向
3. 旋转上向量$\hat{t}$到y轴正方向

可以看出，该变换包含一次平移与两次旋转，两次旋转可以合并为一个旋转变换，所以有：$M_{view}=R_{view}T_{view}$

其中，$T_{view}=\begin{bmatrix}1&0&0&-x_e\\0&1&0&-y_e\\0&0&1&-z_e\\0&0&0&1\end{bmatrix}$

直接求取旋转矩阵较为困难，但我们可以将x、y、z轴变换到相机坐标系，然后求变换的逆。

$R_{view}^{-1} = \begin{bmatrix}x_{\hat{g}\times\hat{t}}&x_t&x_{-g}&0\\y_{\hat{g}\times\hat{t}}&y_t&y_{-g}&0\\z_{\hat{g}\times\hat{t}}&z_t&z_{-g}&0\\0&0&0&1\end{bmatrix}$

对于该变换，我们将其乘以(1,0,0,1)，可以得到向量(x_{g×t},0,0)，即相机坐标系的x轴。对于原y轴和z轴的单位向量，乘以该矩阵以后也能变换到对应的坐标轴。

由于旋转矩阵是正交矩阵，所以其逆矩阵就等于转置矩阵。因此，有：

$R_{view} = R_{view}^{-1} = \begin{bmatrix}x_{\hat{g}\times\hat{t}}&y_{\hat{g}\times\hat{t}}&z_{\hat{g}\times\hat{t}}&0\\x_t&y_t&z_t&0\\x_{-g}&y_{-g}&z_{-g}&0\\0&0&0&1\end{bmatrix}$

所以，我们可以得到，$M_{view} = R_{view}T_{view} = \begin{bmatrix}x_{\hat{g}\times\hat{t}}&y_{\hat{g}\times\hat{t}}&z_{\hat{g}\times\hat{t}}&0\\x_t&y_t&z_t&0\\x_{-g}&y_{-g}&z_{-g}&0\\0&0&0&1\end{bmatrix}$$\begin{bmatrix}1&0&0&-x_e\\0&1&0&-y_e\\0&0&1&-z_e\\0&0&0&1\end{bmatrix}$

投影变换

投影分为正交（Orthographic）和透视（Perspective）。

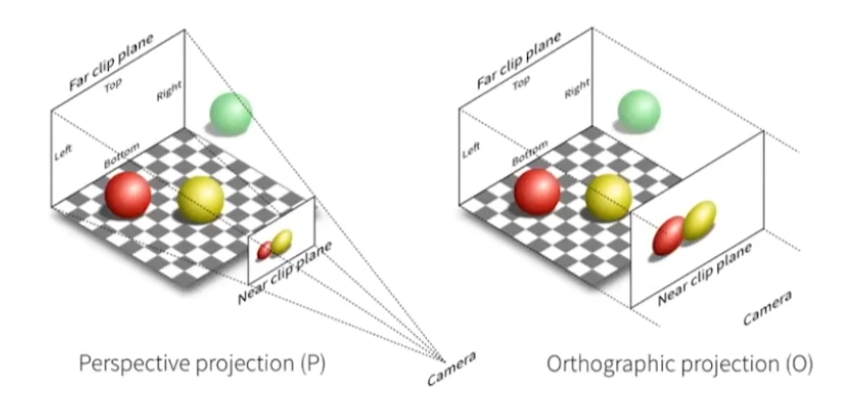
正交投影

本质上是将左右范围为[left, right]，上下范围为[bottom, top]，前后范围为[near, far]的立方体映射到正侧（Canonical）立方体[-1, 1]^3上。

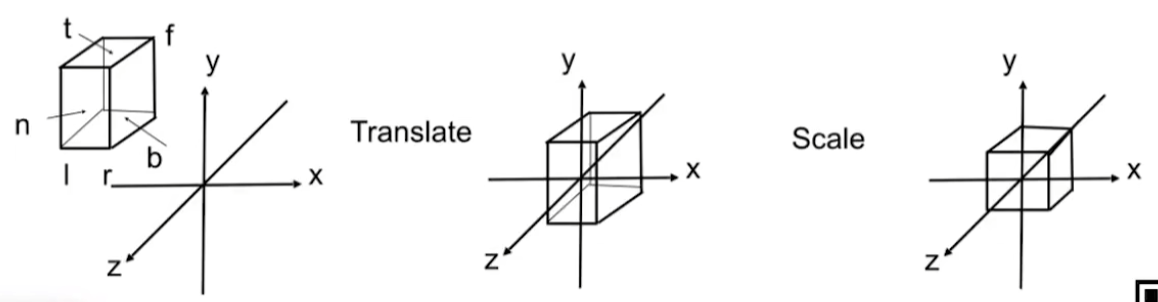
先平移，后缩放：

$M_{ortho} = \begin{bmatrix}\frac{2}{r-l}&0&0&0\\0&\frac{2}{t-b}&0&0\\0&0&\frac{2}{n-f}&0\\0&0&0&1\end{bmatrix}$$\begin{bmatrix}1&0&0&-\frac{r+l}{2}\\0&1&0&-\frac{t+b}{2}\\0&0&1&-\frac{n+f}{2}\\0&0&0&1\end{bmatrix}$

透视投影

通俗理解透视投影，可以将透视变换分为两步：首先，将Far plane “挤压”，使其大小与Near plane一致，这样Frustum就变为了立方体；随后，进行正交投影。

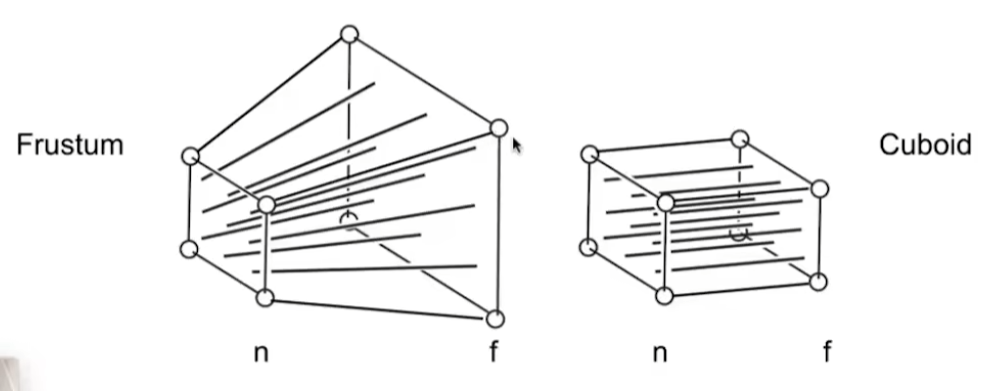
根据相似三角形，我们可以得到：$y’ = \frac{n}{-z}y$，$x’ = \frac{n}{-z}x$

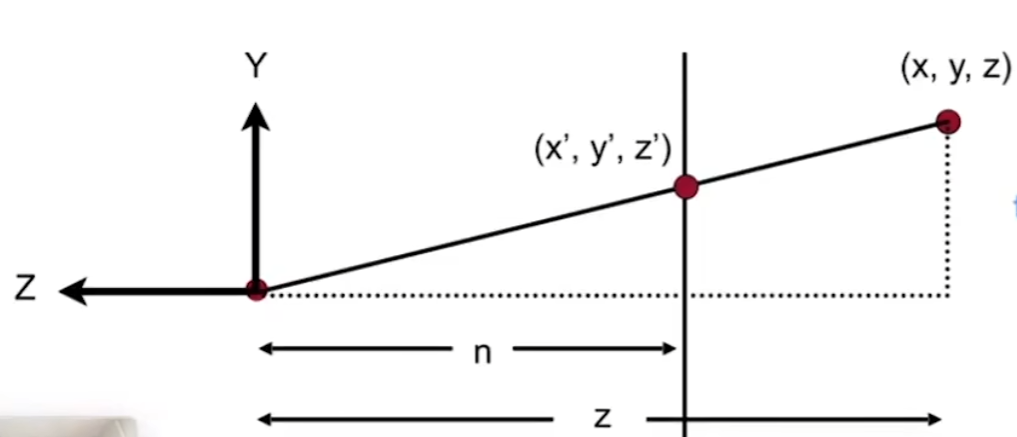
我们知道，在齐次坐标中，有：(x,y,z,w)等价于(x/w,y/w,z/w,1)。由于进行投影后深度信息丢失，而我们需要深度信息进行深度测试，所以我们让w分量等于原来的深度值z，则有：

$\begin{bmatrix}x\\y\\z\\1\end{bmatrix}\Rightarrow$$\begin{bmatrix}\frac{nx}{-z}\\\frac{ny}{-z}\\unknown\\1\end{bmatrix}==$$\begin{bmatrix}nx\\ny\\unknown\\z\end{bmatrix}$

根据上述向量变换规律，我们可以写出部分变换矩阵：

$M_{persp\rightarrow ortho} = \begin{bmatrix}n&0&0&0\\0&n&0&0\\?&?&?&?\\0&0&1&0\end{bmatrix}$

为了推导z’，我们选择一个特例：位于近平面的一个点(x,y,n,1)。经过变换，它应当等价于(nx,ny,n^2,-n)。因此，我们知道变换后的z与x，y都没有关系。

此外，远平面的中心点(0,0,f,1)，经过挤压后仍然是(0,0,f,1)，等价于(0,0,f^2,f)。我们可以列出方程组：

$An+B=n^2, Af+B=f^2$

解得$A=n+f, B=-nf$

因此，$M_{persp\rightarrow ortho} = \begin{bmatrix}n&0&0&0\\0&n&0&0\\0&0&n+f&-nf\\0&0&1&0\end{bmatrix}$

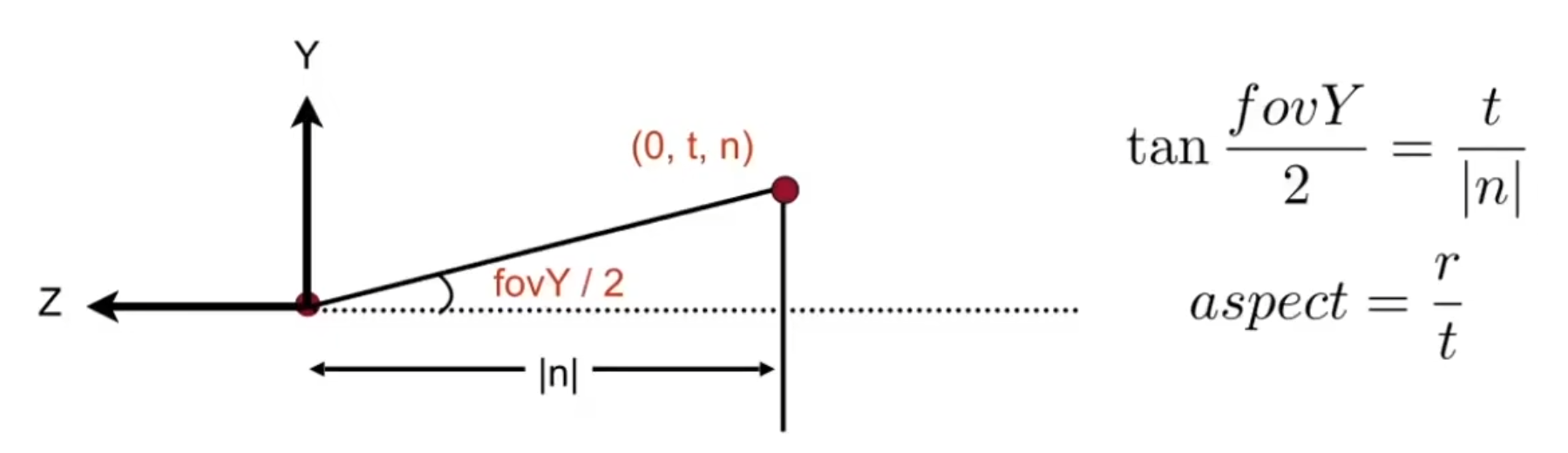
常见的情况下，我们不会直接得到l、r、t、b，而是使用垂直视场角和屏幕宽高比推导出这四个参数：

光栅化

屏幕是一个光栅成像设备（Raster Display Device），它由一个像素（Pixel）数组构成。像素是一个个拥有一致颜色的小方块，它的颜色是由红、绿、蓝三色混合而成的。屏幕像素数组的大小被称为分辨率（Resolution）。

光栅化（Rasterize）通俗来讲，就是将几何体画在屏幕上的过程。

视口变换

屏幕空间（Screen Space）以屏幕为基准，定义了一套坐标系。一般而言，屏幕左下角为原点，向上为Y轴正方向，向右为X轴正方向。

我们使用整数对来描述像素坐标，横坐标为像素左边的像素数，纵坐标为像素下方的像素数。像素(x,y)的中心点实际上位于(x+0.5,y+0.5)。

为了将NDC范围[-1,1]映射到屏幕范围[0,width] [0,height]，我们对NDC坐标做如下变换：

$M_{viewport} = \begin{bmatrix}\frac{width}{2}&0&0&\frac{width}{2}\\0&\frac{height}{2}&0&\frac{height}{2}\\0&0&1&0\\0&0&0&1\end{bmatrix}$

该变换被称为视口变换（Viewport Transformation）。

三角形

三角形是最基础的多边形，任何多边形都可以被分解为三角形。三角形具有以下独特性质：

• 三角形上的所有点都处于同一平面
• 三角形的内外分明，不会出现凸、凹多边形的情况
• 三角形的三个顶点的顶点属性确定时，内部任意一点的顶点属性都能通过插值得出。

我们使用采样（Sampling）的方式将三角形光栅化为屏幕上的像素：

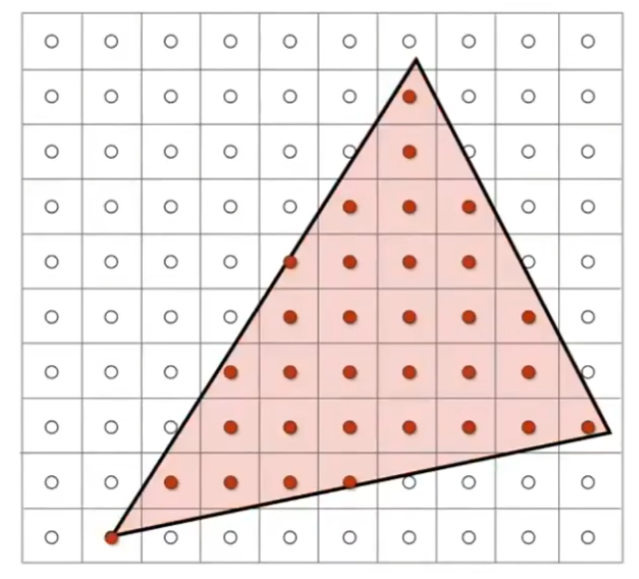
一种简单的方法是，遍历屏幕上每个像素的坐标，若坐标(x+0.5),(y+0.5)位于三角形内部（使用叉乘同号判断），则该像素设置为三角形颜色。

注意点：

• 叉乘时，按照一定的顺序构造向量。如P1，P2，P3，构造时便是P1-P2与P1-Q叉乘，P2-P3与P2-Q叉乘，以此类推，不能中途反过来。
• 当点位于三角形边的时候，有一次叉乘会是0。这种情况，既可以不做处理，也可以特殊处理。

如果对于每个三角形，都遍历屏幕上的所有像素，性能消耗较大。因此，我们为每个三角形设置一个包围盒（Bounding Box ，又称Axis-Aligned Bounding Box，轴向包围盒，AABB），包围盒由三个顶点的坐标定义，每次遍历仅遍历包围盒内部的像素。

反走样

由于一个像素只能显示一种颜色，光栅化后的三角形会出现锯齿化边缘。这种现象被称为走样（Aliasing）。优化这种现象的技术被称为反走样技术（Anti-Aliasing）。

瑕疵（Artifacts）泛指图形学中的一切错误显示现象。走样是瑕疵的一种。除此之外，还有摩尔纹、车轮效应等瑕疵。这些瑕疵都是采样导致的。

走样本质上是“信号变化太快，采样速度太慢”导致的。

在光栅化之前，对三角形进行模糊处理，可以一定程度上缓解走样：

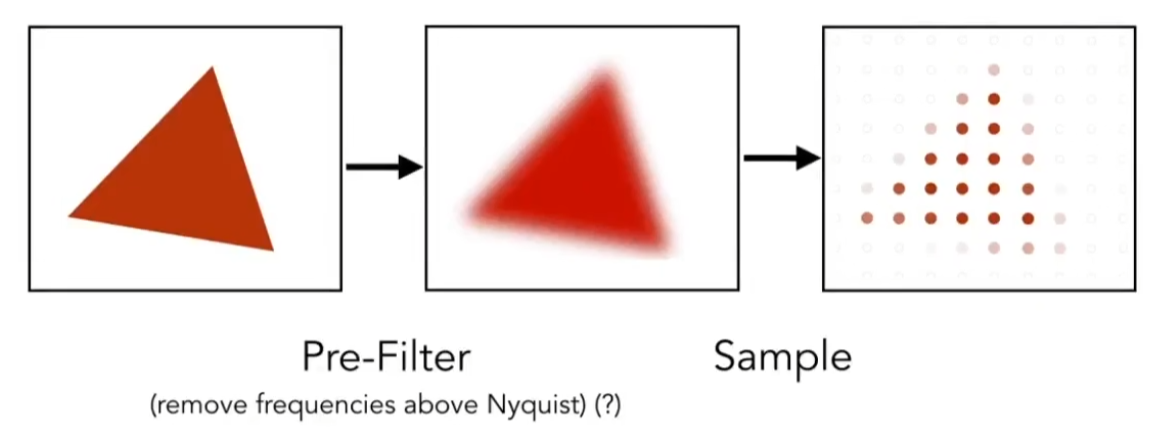
这类方法必须在采样之前做模糊。如果将顺序颠倒，则依然会出现走样的情况，此时的走样被称为模糊走样（Blurred Aliasing）。

频域

对于余弦函数$cos2\pi fx$，$f$称为该函数的频率（Frequency），$T = \frac{1}{f}$称为该函数的周期。

傅里叶变换（Flourier Transform）表示能将满足一定条件的某个函数表示成三角函数（正弦和/或余弦函数）或者它们的积分的线性组合。其本质是把一个函数分解为不同的频率。

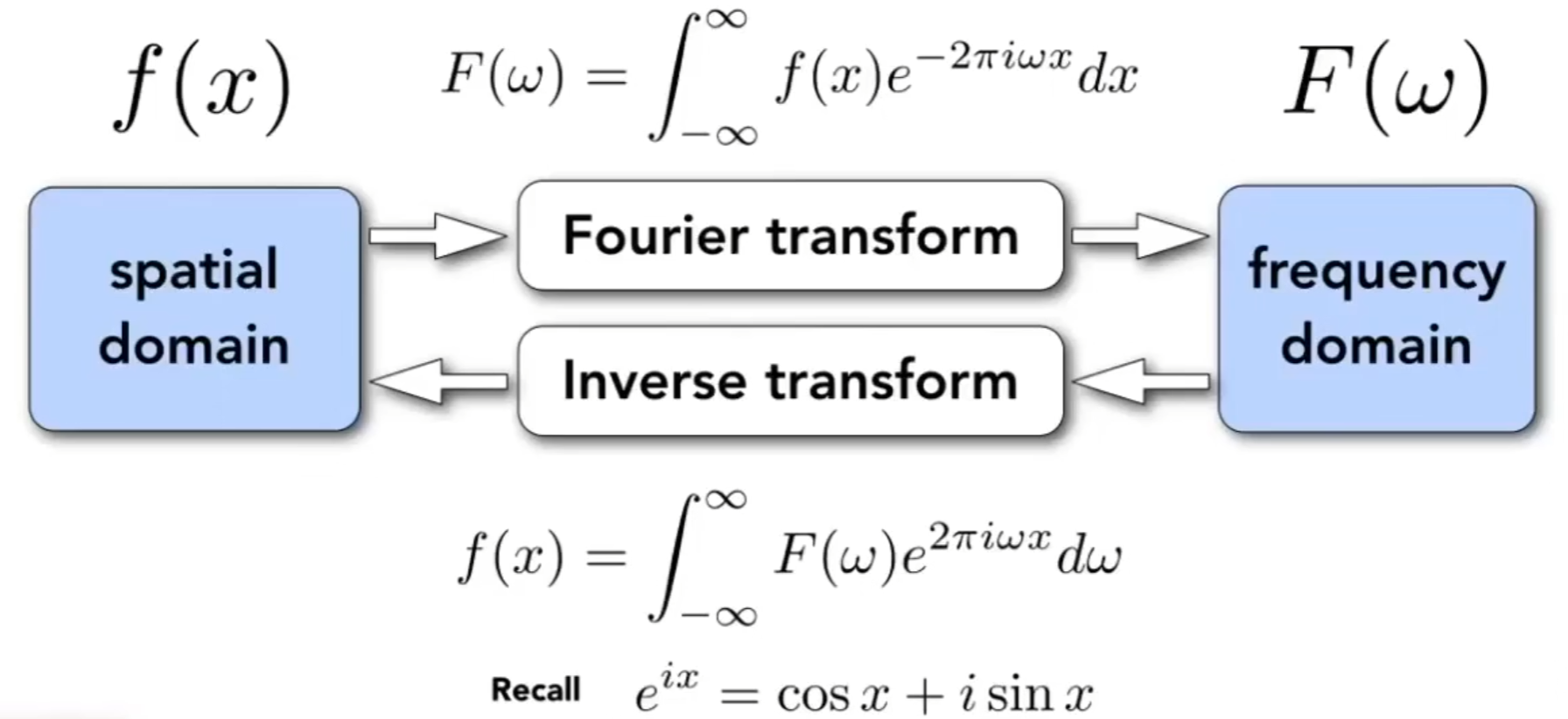
走样的本质是：采样两个频率完全不同的函数，得到的是相同的结果。

滤波（Filtering）指将特定频率的信号过滤掉。

图像在时域中表示为像素的二维矩阵，其中每个元素代表图像中某个点的亮度或颜色。时域中可以直观地看到图像的细节，例如物体的形状、边缘等。频域表示的是图像中不同频率的成分。傅里叶变换将时域中的每个像素值重新表示为一组频率的组合。频率指的是图像灰度或颜色变化的快慢，低频表示图像中的大范围平滑变化（如均匀的区域），高频表示快速变化的部分（如边缘、细节等）。

高通滤波器（High-Pass Filter）指能将图像中高频（颜色变化较快）的部分滤出的滤波器。它可以提取出图像的边界。

低通滤波器（Low-Pass Filter）能将图像中低频（颜色变化平缓）的部分滤出的滤波器，它可以将图像的边缘模糊。

卷积

在图形学领域，过滤=卷积=平均。

何为卷积？

在移动滑动窗口的过程中，将窗口内的值与窗口覆盖的原始信号的值做点乘：

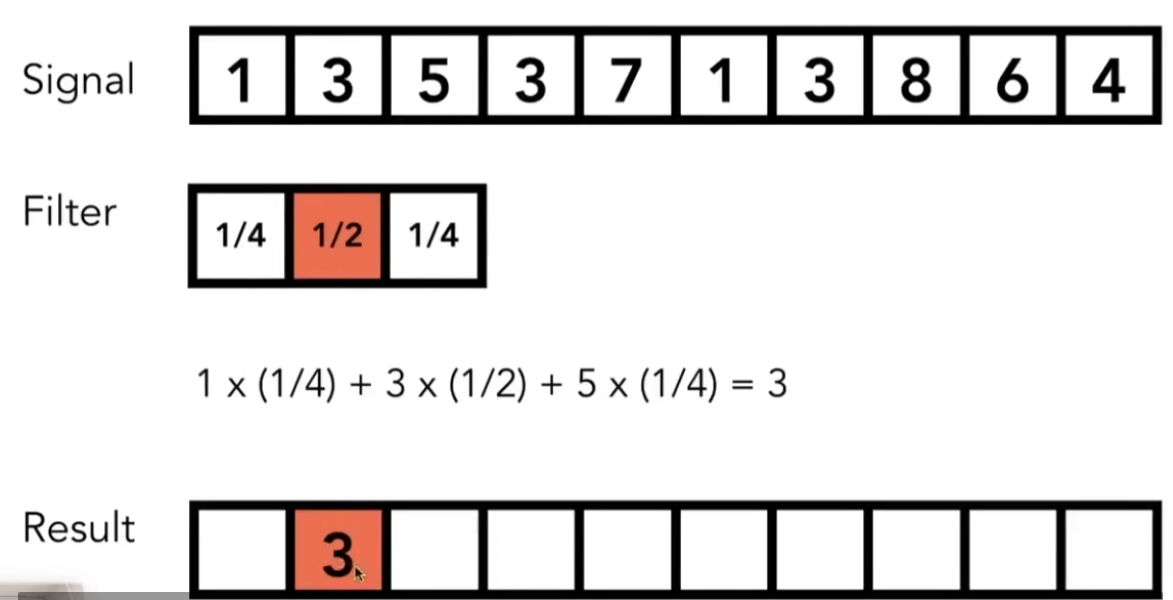
反走样技术

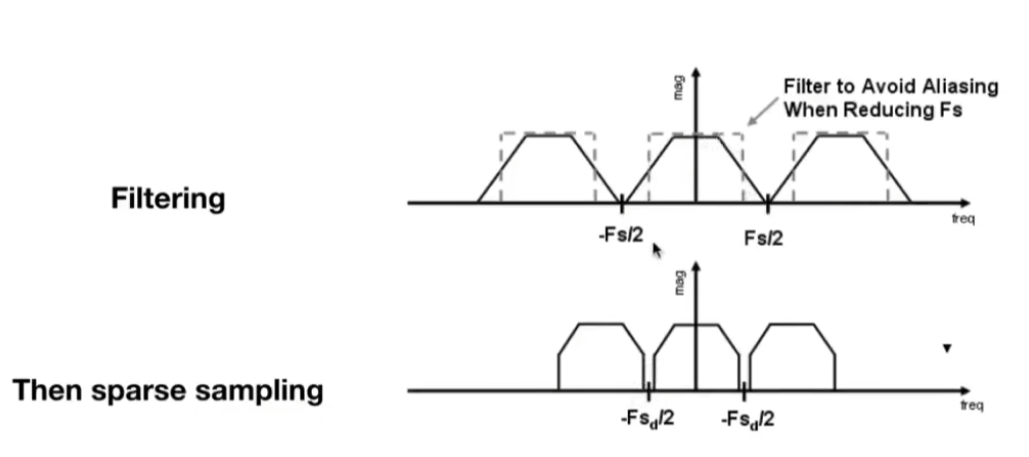
1. 增加采样率，提高屏幕分辨率、传感器精度、帧缓冲数量等
2. 在采样之前对信号进行低通滤波，在图像处理方面表现为对图像进行卷积平均

着色

着色（Shading）指对物体应用材质的过程。

Blinn-Phong反射模型

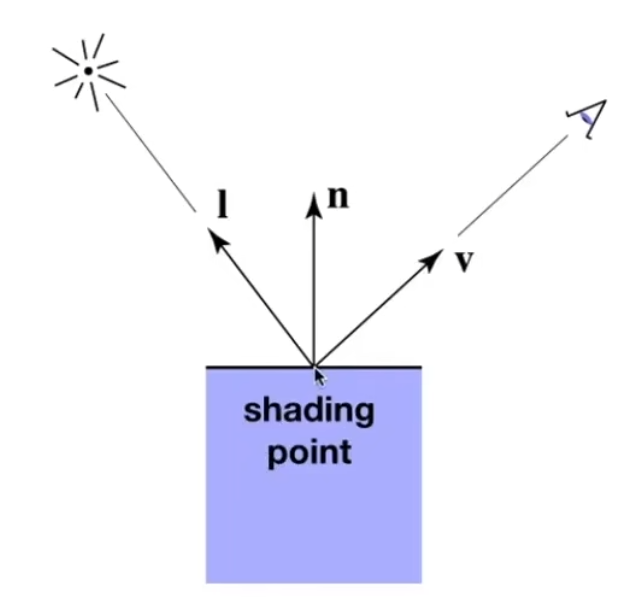
漫反射

对于漫反射（Diffuse）光，光照向量I与法向量n的夹角越小，着色点接收到的光照能量就越大，漫反射光就越强（Lambert定律）。

对于点光源，假设距离光源中心1单位的点的光强为I，则距离光源中心r单位的点的光强为I/r^2。因此，我们可以写出漫反射光分量强度：

L_d = k_d(\frac{I}{r^2})max(0,\symbf{n\ ·\ l})

其中，$k_d$为漫反射颜色系数，$I$为光源强度,$n$为法向量，$l$为光照方向。

镜面反射

对于镜面反射（Specular）光，视角方向越接近镜面反射光，就越亮。

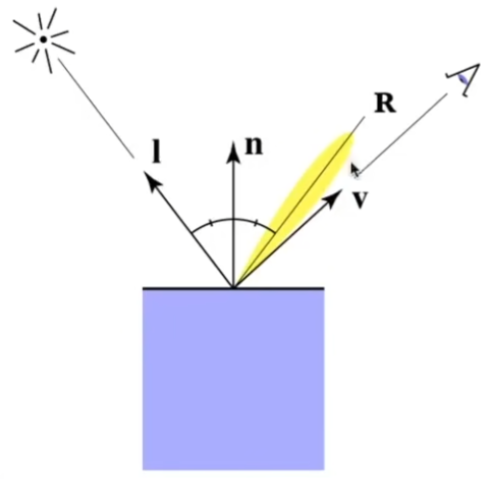
我们可以发现，当视角方向越接近镜面反射光时，半程向量（Half Vector，光照方向和视角方向的平分向量）就越接近法向量。即：

L_s = k_s(I/r^2)max(0,cos\alpha)^p = k_s(I/r^2)max(0,\symbf{n · h})^p

其中\symbf{h}为半程向量，$h = \frac{\vec{v}+\vec{l}}{||\vec{v}+\vec{l}||}$；$p$为反射度，越大则镜面反射范围越小，一般用100-200。

使用半程向量是因为，比起计算反射方向，半程向量的计算量小得多。同时，使用半程向量也能确保拥有镜面反射的着色点会更多，不会出现明显的断层现象。

环境光

对于环境（Ambient）光，在Blinn-Phong模型中，我们认为每一点的环境光都相同：

$L_a = k_a I_a$

将三个光照分量组合，即可得到完整的光照：

$L = L_a+L_d+L_s = k_a I_a + K_d (I/r^2) max(0,\vec{n}·\vec{l})+k_s (I/r^2) max(0,\vec{n}·\vec{h})^p$

着色频率

着色频率（Shading Frequencies）指在图形渲染过程中，着色操作执行的频率。着色频率决定了着色的精细程度和计算资源的消耗。

常见的着色频率包括‌：

• 逐面着色（‌Flat Shading） - 每个三角形只有一个法向量，对于平滑曲面效果不佳。
• 逐顶点着色（‌Gouraud Shading） - 每个顶点有一个法向量。
• 逐像素着色（‌Phong Shading）。‌

当模型的顶点数增多时，三种着色频率最终的输出差异会越来越小。当顶点数增大到某种程度时，Flat Shading/Gouraud Shading的计算量甚至会超过Phong Shading.

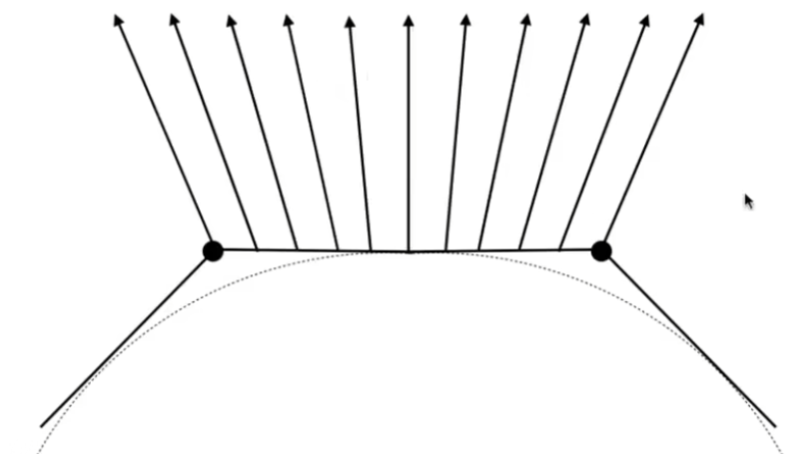
我们知道，每个顶点都会与多个三角形有关。因此，在Gouraud Shading中，每个顶点的法线通过对周围三角形的法线求平均获得：$N_v = \frac{\sum_iNi}{||\sum_i Ni||}$

一种优化方式是进行加权平均，以三角形的面积为权重。

在Phong Shading中，我们已知每个顶点的法线，通过重心插值法（Barycentric Interpolation）来获取每个片段的法线。

实时渲染管线

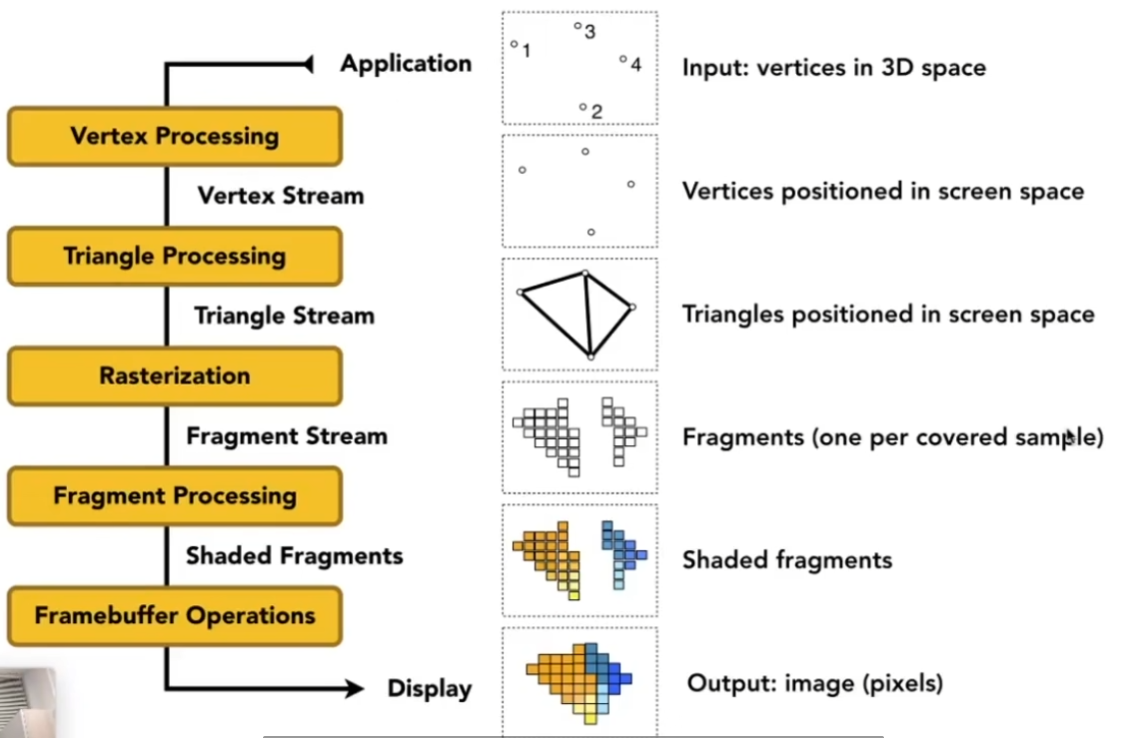
着色器程序

着色器（Shader）是对顶点和片段进行逐次处理的通用着色程序。

纹理映射

纹理映射（Texture Mapping）本质上用于定义每个片段的漫反射系数、深度值等基本属性。

纹理坐标（Texture Coordinates）用于将几何体上的三角形映射到纹理上。

UV的范围是[0,1]。

重心坐标

重心坐标（Barycentric Coordinates）用于三角形内部的插值。

对于三角形，顶点属性在三个顶点是确定的。但在实际着色中我们需要三角形上每个像素的属性，这些属性由顶点属性插值获取。

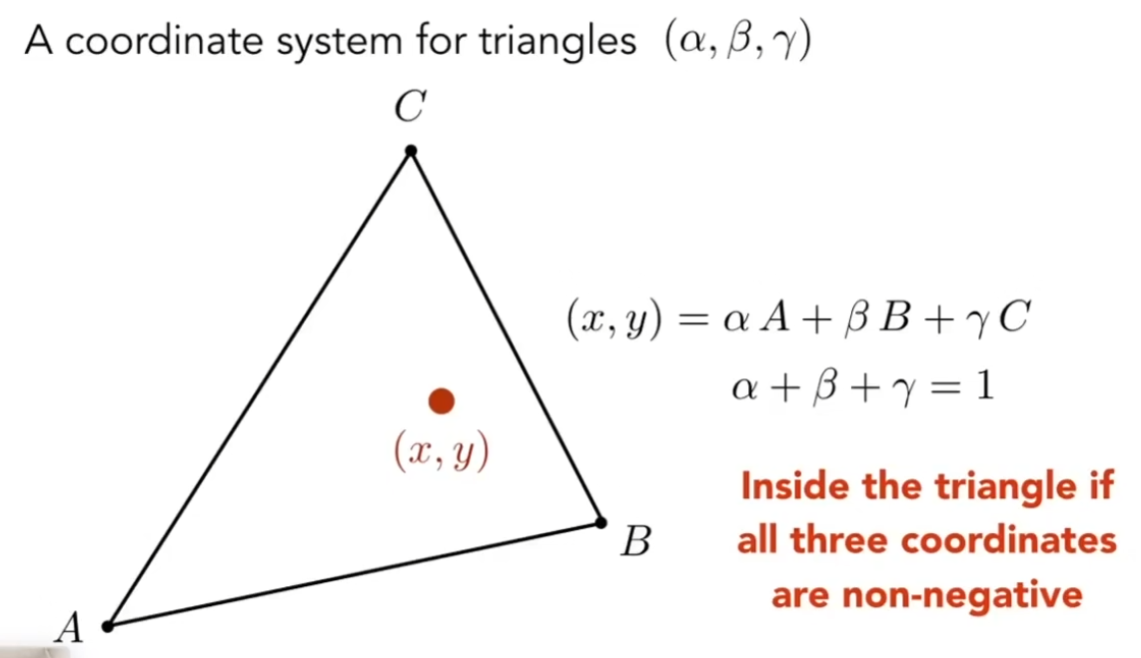
如图，式内A、B、C为三点的坐标。对于任意用A、B、C表示坐标的点，只要系数$\alpha+\beta+\gamma=1$，并且三个系数均为正，则该点在三角形内。此外，$\alpha、\beta、\gamma$的值也可以用三角形面积比值求出：

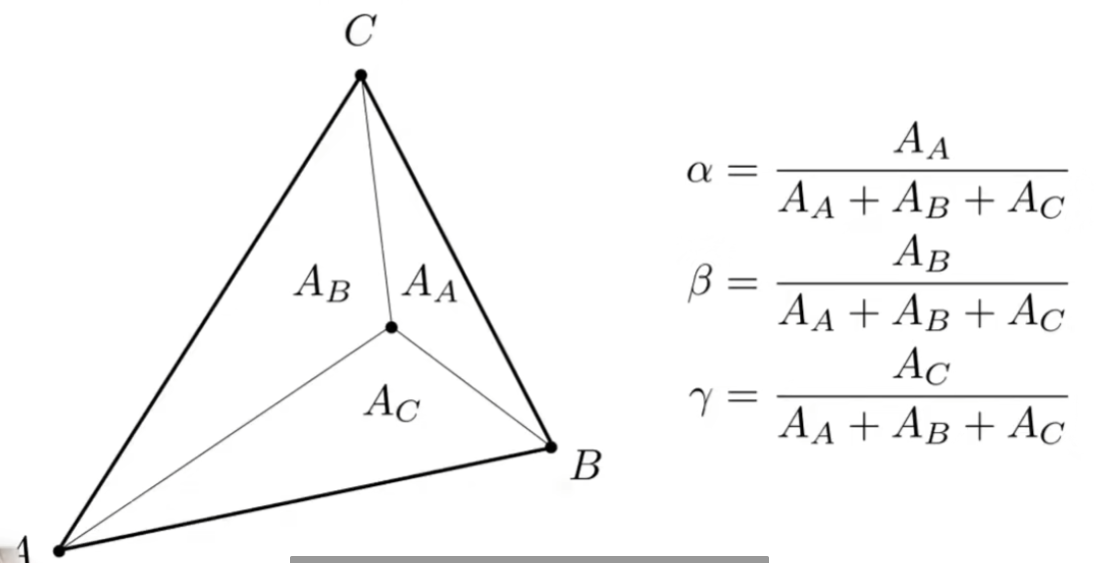
三角形的面积可以由叉乘公式求出，如$S_{A_B} = \frac{1}{2}|\vec{AC}\times\vec{AP}|$，如果将该公式用具体坐标化简，可得：

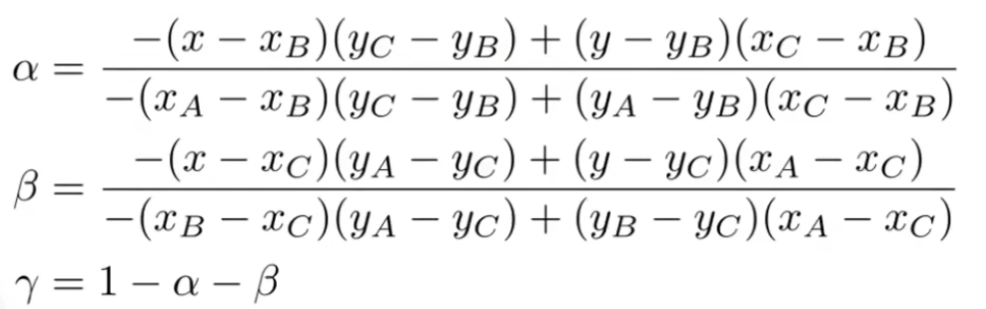
对于该点，$(\alpha, \beta, \gamma)$就是它的重心坐标，三个参数分别是该点对于点A、B、C的插值系数。例如，点A的颜色为a，点B的颜色为b，点C为c，则插值后该点的颜色就是$(\alpha a, \beta b, \gamma c)$

需要注意的是，重心坐标经过投影变换后会发生变化，因此，若需要插值三维坐标，则需要在投影前进行重心坐标计算。对于深度计算，则需要在投影后，对各像素对应的三角形顶点应用逆投影变换，然后插值得到深度。

应用纹理

将一个低分辨率纹理应用到高分辨率物体上，会出现多个屏幕像素（Pixel）对应纹理上同一个纹素（Texel）的情况。此时，就需要决定像素-纹素的映射方式。

• Nearest方式直接将屏幕像素映射到最近的纹素上。

• Bilinear方式：使用双线性插值（Bilinear Interpolation），该方法寻找邻近的四个纹素，将四个纹素的中心点框选出一个矩形，并以采样点到左边的距离s作为比例（s必定小于1，若大于1就会框选另外的纹素了），分别对上面的两个纹素和下面的两个纹素进行线性插值，得到两个颜色值。随后，以采样点到下面的距离t作为比例，对先前得到的两个颜色值进行插值：

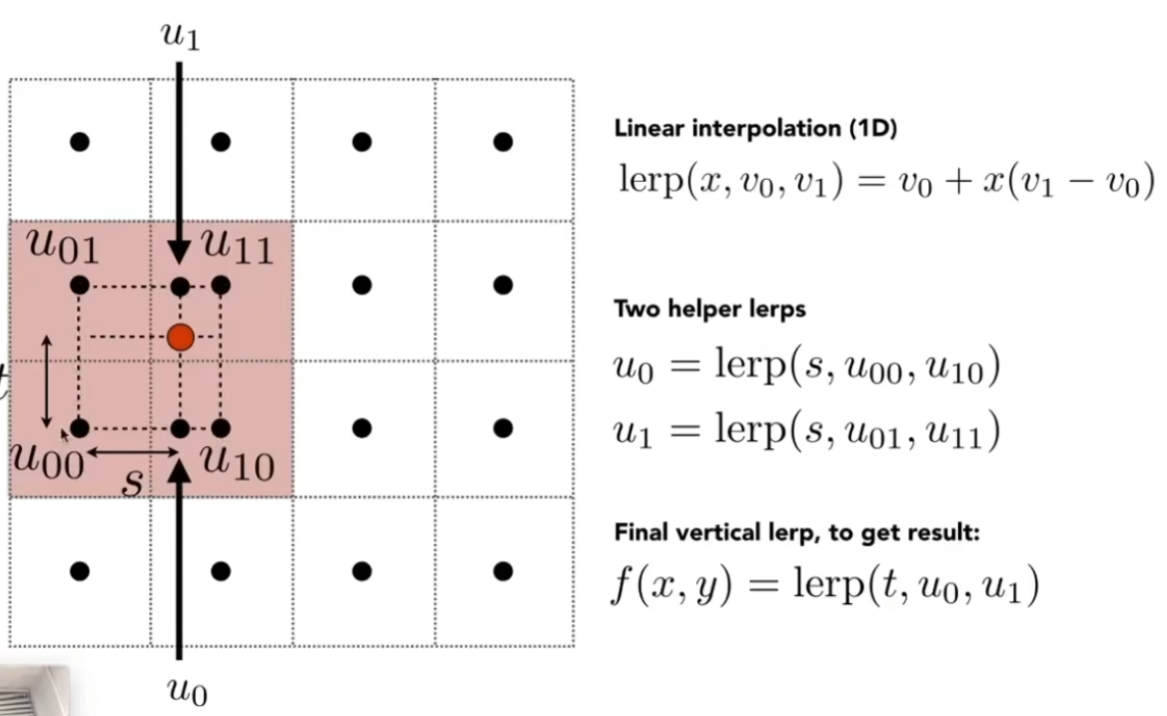
• Bicubic方式：使用双三次插值，寻找周围的十六个纹素，每次使用四个纹素坐标进行插值。

相对地，将大纹理应用到小平面，当一个像素远大于纹素时，会出现摩尔纹，因为采样时可能会跳过一些纹素。

一种解决方法是提高采样频率，但开销过大。

另一种方法是避免采样，对纹理进行预处理，使其处于不同的远近层次时，具有不同的细节层次。三角形越远，则纹理越模糊（越多的纹素被取平均值）。这种技术被称为多级渐远纹理（Mipmap）。

Mipmap是一种快、近似、仅适用于正方形的范围查询方式。一个纹理可以生成若干个Level的Mipmap，Level越高，Mipmap的分辨率越小。

如何计算纹理的大小？

取光栅化后三角形上两个相邻的点P1、P2，比较这两个点之间的距离和UV坐标之间的距离。

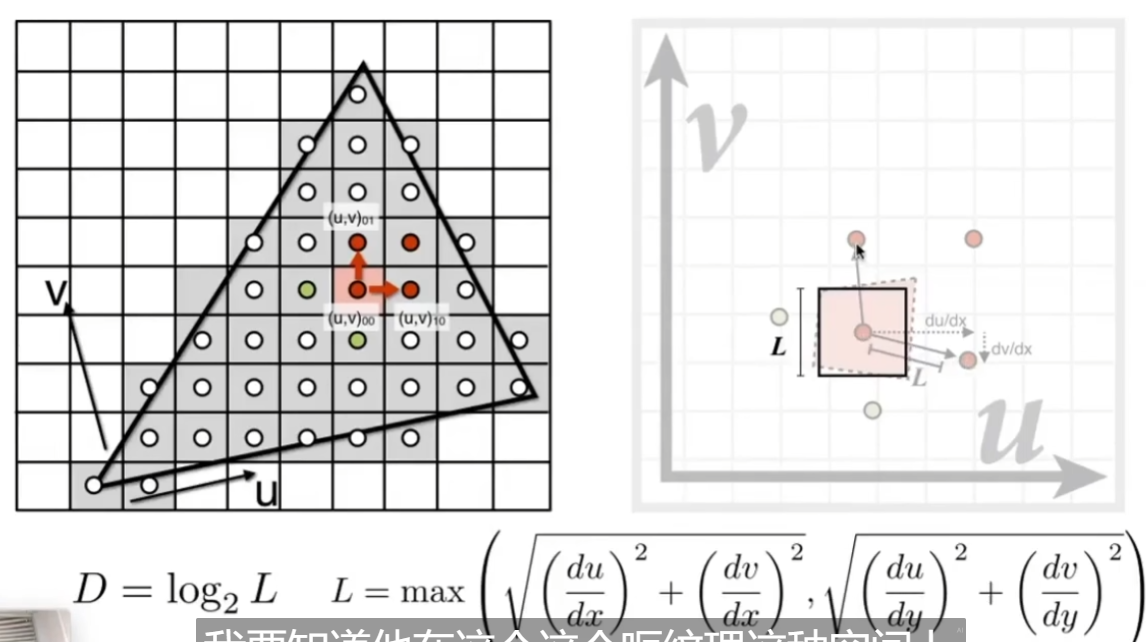
完成比较后，我们便能得到，一个像素在纹理上放大后约等于多少纹素。在上图中，一个纹素=2*2像素，我们便可以选取Level 1级别的Mipmap进行采样。

但是，不同级别的Mipmap如果简单过渡的话，会出现断层问题。因此，我们对Mipmap也可以采用三线性插值：

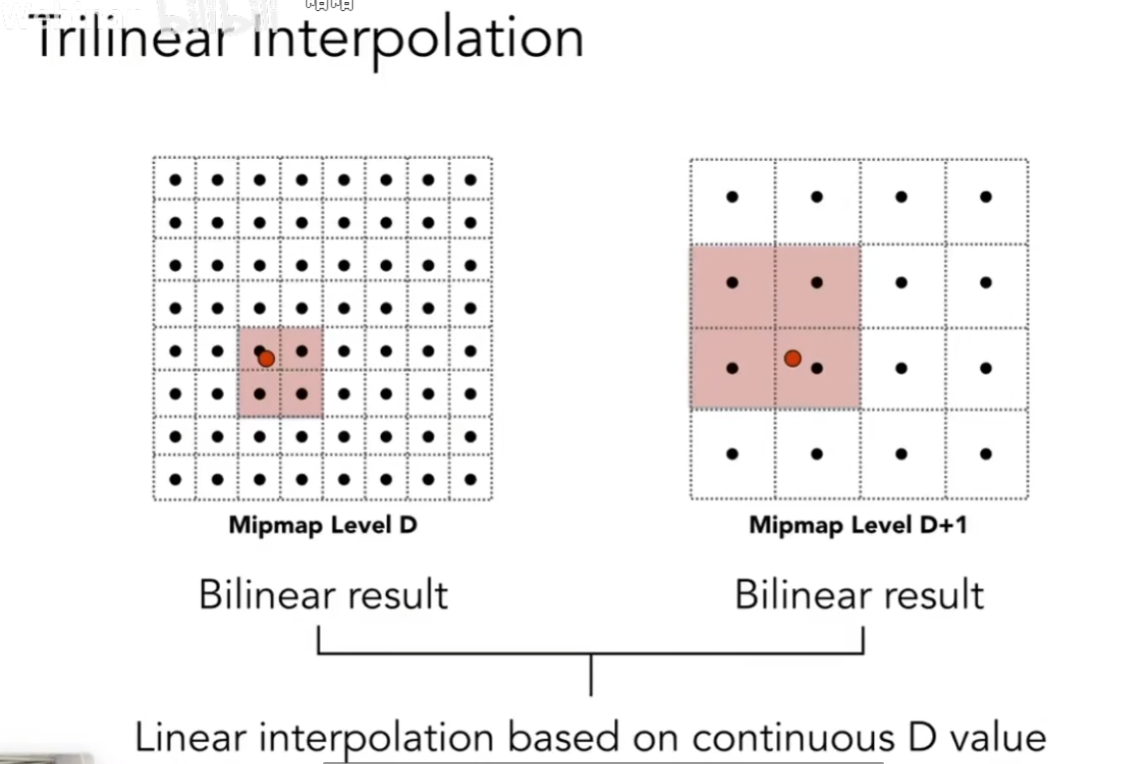
在层内部使用双线性，在不同层之间使用单次线性插值，共计三次线性插值。

Mipmap的缺点之一是，它会将远处的几何体纹理的细节过度模糊（Over blurred），这是由Mipmap各级的颜色平均操作和三线性插值的近似性引起的。

我们在计算像素/纹素比例时，会将纹理在屏幕上一个像素内部的显示区域近似为一个正方形。但实际上，在视角变化时，可能会难以近似。例如：

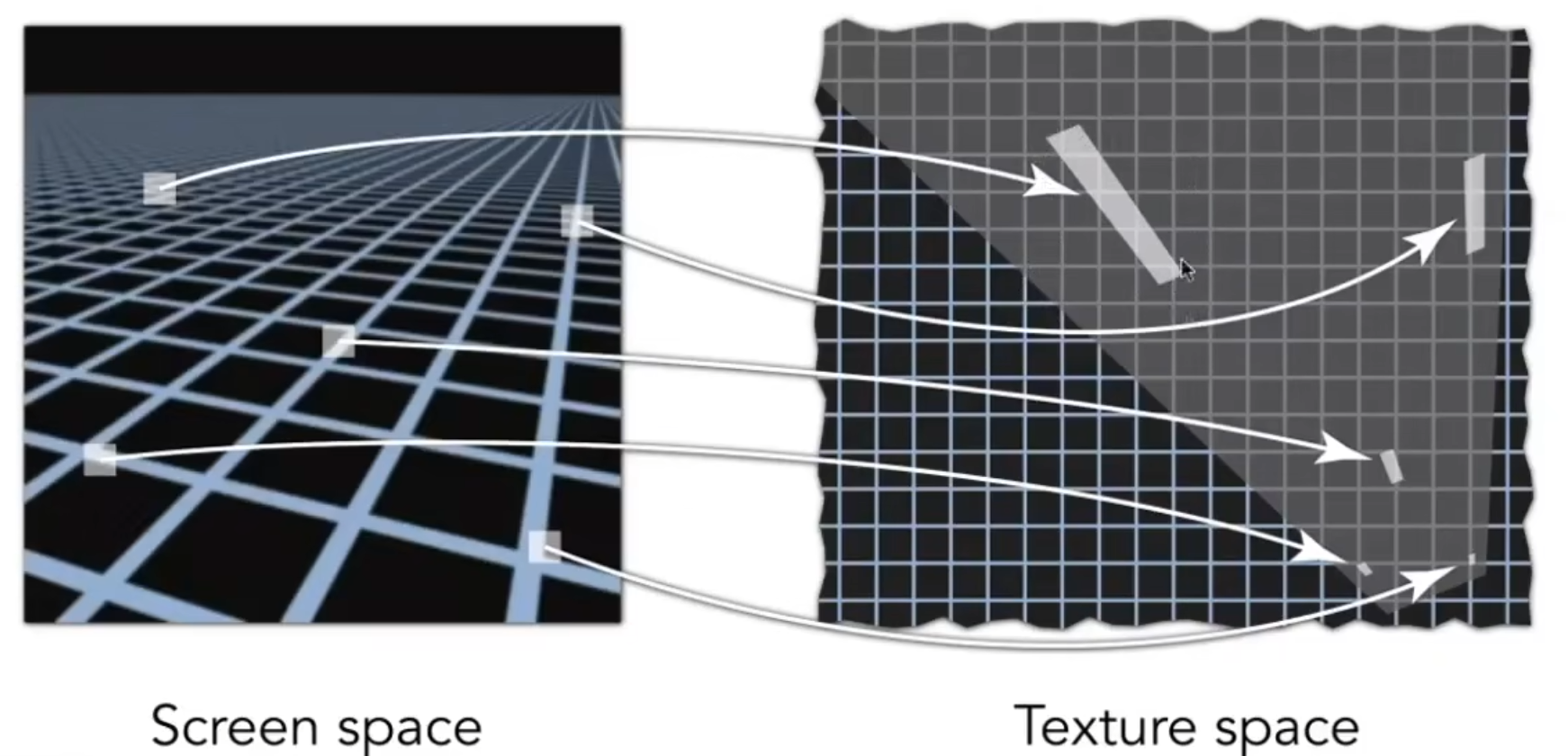
此时，如果想用一个正方形把拉长的四边形框住，就会框住更大的区域，把更多的颜色平均，导致模糊。

各向异性过滤（Anisotropic Filtering）用于解决Mipmap的这一缺点，在生成正方形Mipmap时同时生成长宽比不同的压缩纹理（被称为Ripmap）。这种方式效果比Mipmap好，但会生成更多的次级纹理，占用更多的显存。Nx各向异性过滤表示生成到$log_2 N-1$ Level的压缩纹理。如图：

对于映射后呈长条形的纹理区域，可以查询长宽比不同的压缩纹理。但如果纹理区域又长又斜的话，就不太能框住。EWA过滤解决了这一问题，它将不规则的区域拆分成规则区域做多次查询，但计算量大。

纹理应用

环境贴图

环境贴图（Environment Map）用于描述环境光分量。它假设环境光仅包含方向信息，都来自无限远处。

球形环境贴图（Spherical Environment Map）将环境贴图以球体贴图的形式保存，环境光分量被记录在球上。

、

但是，这类贴图展开后会导致上下两边变形。为了解决这一问题，我们引入立方体贴图（Cube Map）。

立方体贴图

每个Cube Map由六张正方形贴图组成。采样Cube Map时，需要先判断方向向量在立方体的哪个面上，再对那个面进行采样。

凹凸贴图

凹凸贴图（Bump Mapping）用于在不添加三角形的情况下为表面添加更多细节。

凹凸贴图定义了不同位置的高度，在光照计算中，通过计算邻近的高度差来重新计算法线。

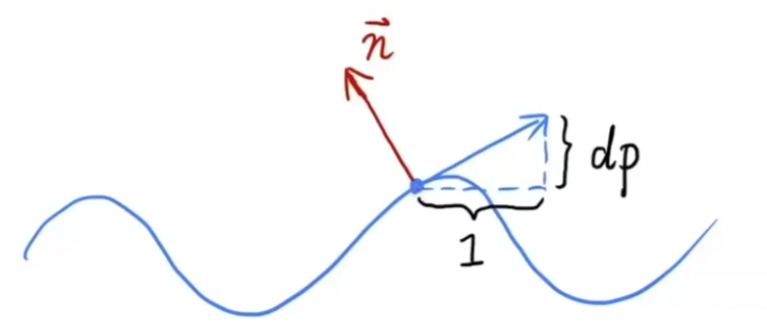
如图，要计算法线$\vec{n}$，就需要知道点P处的切线。假设两个相邻的点，距离1，它们的高度差为h(p+1)和h(p)，则切线斜率为h(p+1)-h(p)。法线垂直于切线，将切线旋转90度即可得到法线。

在三维空间中，我们可以分别求u、v两个方向的切线，即可得到法线：

位移贴图

位移贴图（Displacement Mapping）存储了顶点的偏移信息。使用位移贴图时，顶点确实被位移了，因此，该类贴图只适合顶点较多的模型。

阴影

最常见的产生阴影的技术是阴影映射（Shadow Mapping）。

关键思想：不在阴影内的片段必定能被从光源视角和相机视角被“看到”（即未被遮挡）。

进行阴影映射的步骤：

1. 从光源位置出发，生成一张深度图。
2. 从相机视角正常渲染。
3. 将相机视角观察到的顶点重新投影到光源视角，对深度图进行采样。若该顶点在光源空间内的深度大于采样到的深度，则该点位于阴影内。

阴影映射技术只能生成硬阴影，即边缘非常锐利的阴影。软阴影效果更好，它在物体根部较为锐利，在物体上部较为模糊。软阴影的本质上是物理中的半影，是由于光源（有一定大小）被部分遮挡而导致的。

几何

显隐式几何

图形学中，几何可分为隐式（Implicit）几何和显式（Explicit）几何。

隐式几何仅表明点之间的特定关系，如使用$x^2+y^2+z^2=1$表示的球面。一般地，我们定义：对于点$(x,y,z)$，只要其满足$f(x,y,z)=0$，则认为该点在函数所表示的表面上。

除了解析式外，还有:

• 构造立体几何（Constructive Solid Geometry，CSG），使用基本几何体的集合运算构造复杂几何体：

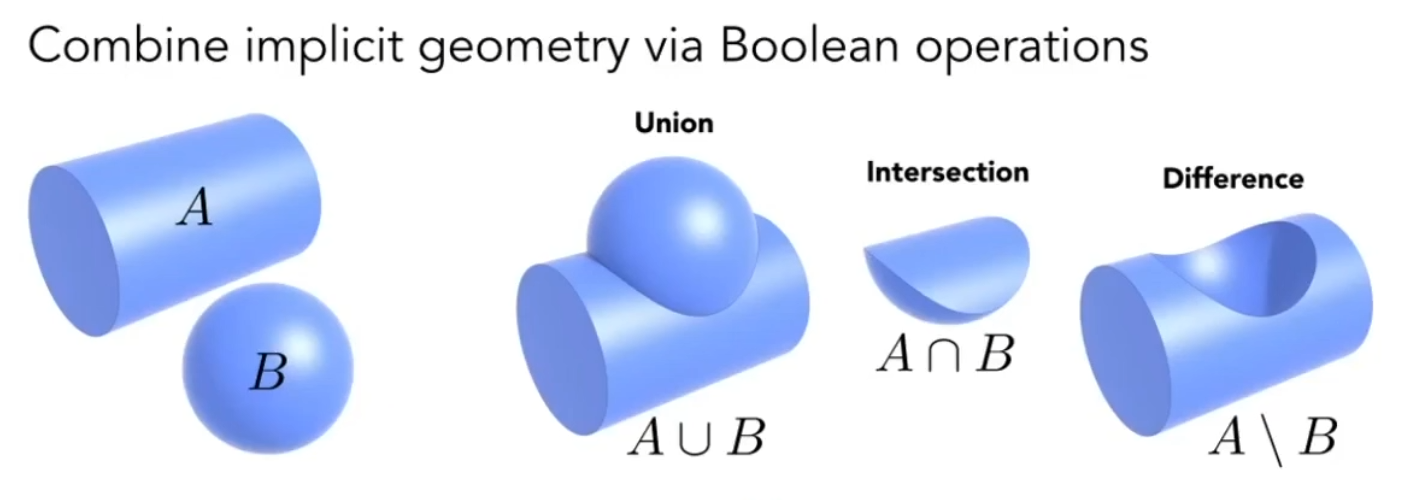
• 距离函数（Distance Functions），不直接描述点，而是描述某处到集合表面的最近距离（有符号，外面为正，内部为负）。
• 分形（Fractals），自相似。

对于隐式几何，想要从解析式判断其形状较为困难，但判断一个点是否在表面上非常简单。

显式几何会给出所有点的坐标，或通过参数映射的方式定义表面。

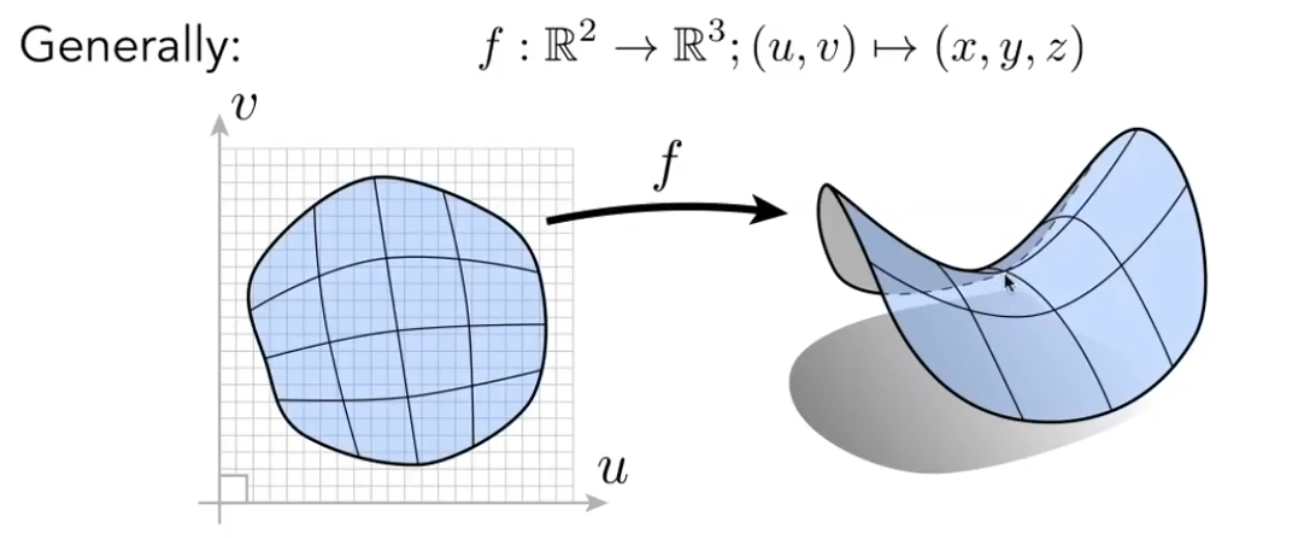
如图，对于参数映射类的显式几何，一般会给出类似于下面的表达式：

$f(u,v) = ((2+cosu)cosv,(2+cosu)sinv,sinu)$

该表达式便定义了一个曲面。通过获取几何体的u、v坐标（已知），即可得到其三维空间坐标。

对于显式几何，想要判断点是否在表面内是非常困难的。

除此之外，常见的显式几何还有：

• 点云（Point Cloud），给出一系列点的三维坐标
  • 没有点之间的关系，所以要表示三维几何体需要很多密集的点
  • 在三维扫描与重建中较为常用
  • 对于大型数据集非常实用
• 多边形网格（Polygon Mesh），给出顶点坐标和多边形（以索引的方式）
  • 图形学中最广泛应用

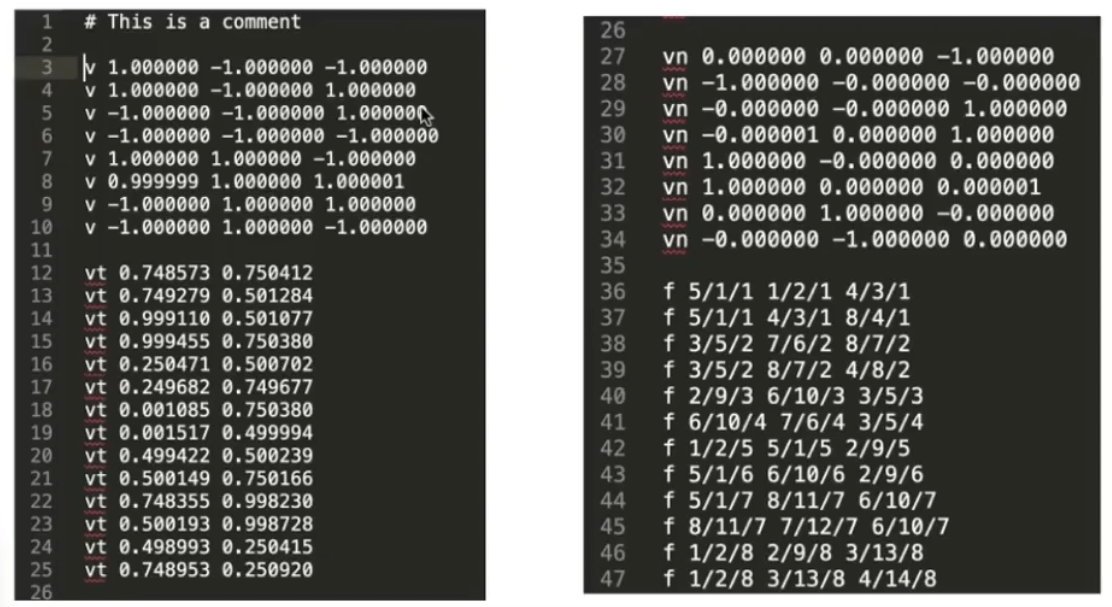
以Wavefront Object File（.obj）格式为例，是一类文本文件，将顶点坐标、法线、纹理坐标和各属性之间的关系等写入文件。

曲线

贝塞尔曲线

贝塞尔曲线（Bezier Curve）用一系列控制点定义一个曲线。

对于三个控制点的情况，可以画出二次贝塞尔（Quadratic Bezier）曲线。

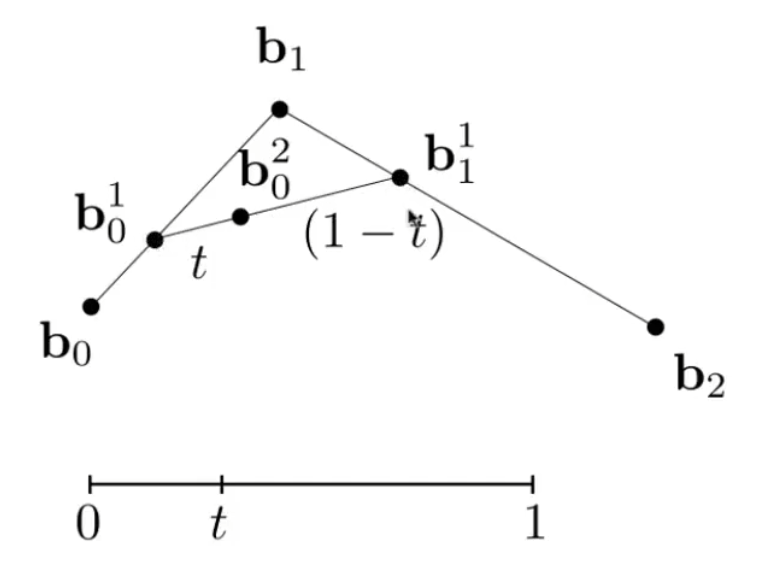
如图，假设时间=t时，线段$b_0b_1$上有点$b_0^1$（其与b0距离占总线段的t），线段$b1b2$上有点$b_1^1$（其与b1距离占总线段t），而线段$b_0^1b_1^1$上有点$b_0^2$（其与$b_0^1$距离占总线段长的t），则在t时刻，点$b_0^2$在贝塞尔曲线上。将t从0遍历到1，就可以画出贝塞尔曲线。

对于四个控制点的情况，存在三个线段，分别找出各个线段上到对应点距离比例为t的点，即可转换到三个控制点的情况。

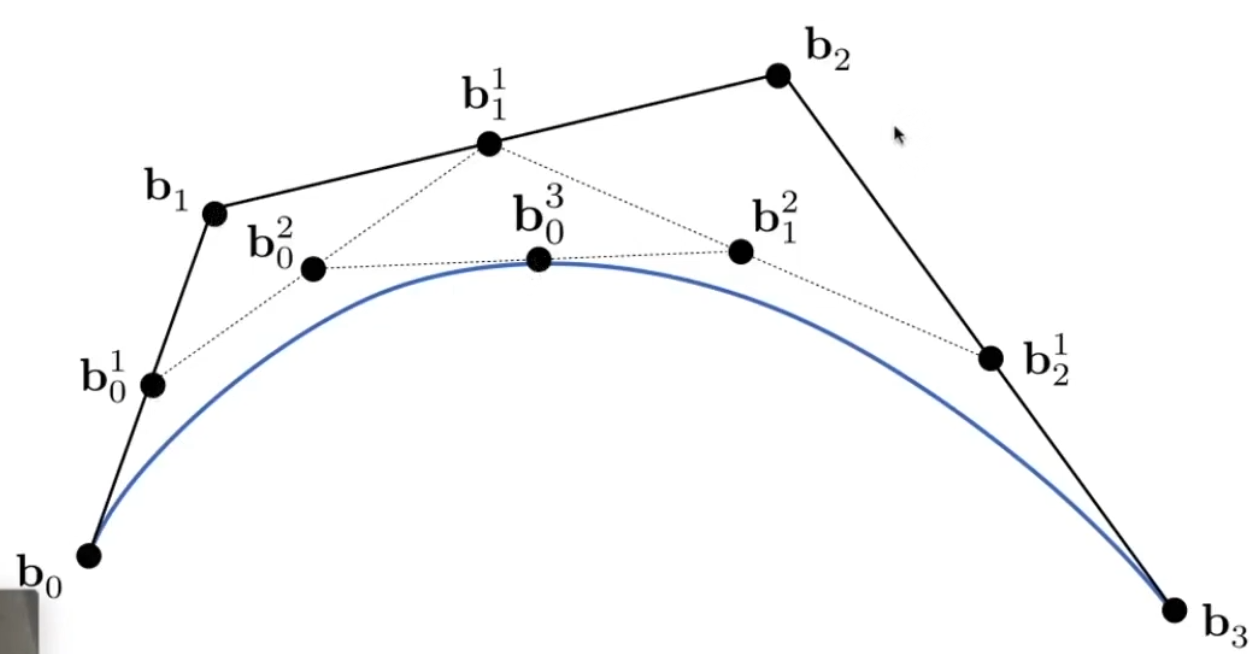
对于更多控制点的情况，也是类似，层层递归。我们可以把这个过程写成代数公式：

$b^n(t)=b_0^n(t)=\sum\limits_{j=0}^nb_jB_j^n(t)$

其中，B被称为伯恩斯坦多项式（Bernstein Polynomial），其值为：$B_i^n(t)=C^i_nt^i(1-t)^{n-i}$

例如，我们要求三个控制点的贝塞尔曲线解析式：

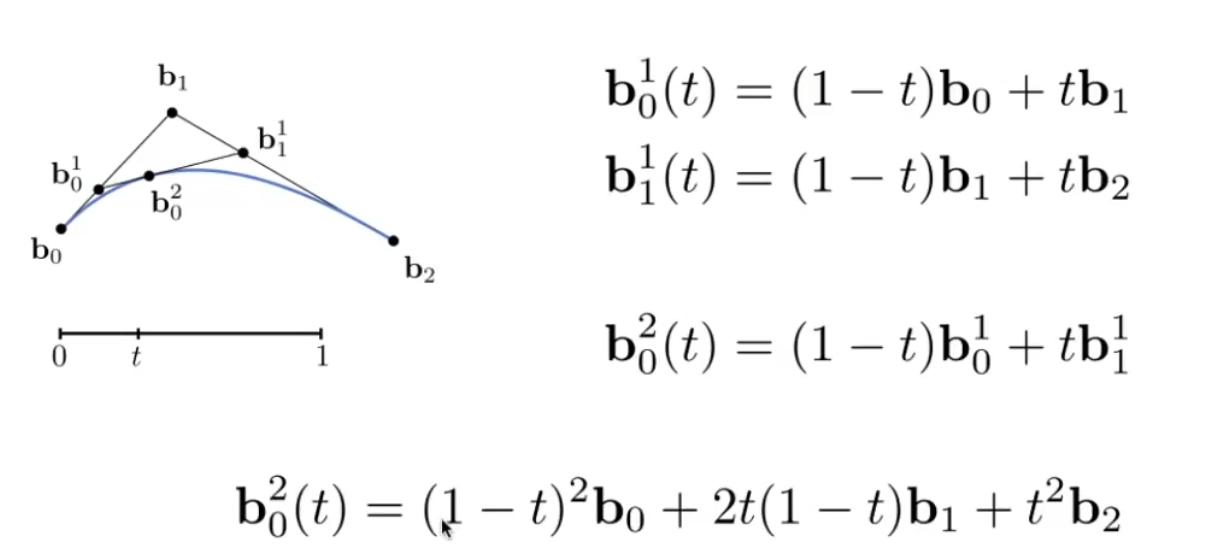
贝塞尔曲线有如下性质：

1. 曲线在t=0时必定在起点，在t=1时必定在终点
2. 顶点的相对位置相同（前后经历了仿射变换），则画出来的贝塞尔曲线的形态完全相同。
3. 贝塞尔曲线必定位于控制点形成的凸包（Convex Hull）内。凸包指若干个点形成的最小凸多边形。

逐段贝塞尔曲线

当控制点增多时，调整单个控制点很难让曲线变成开发者想要的形态。为了解决这一问题，我们可以逐段地定义贝塞尔曲线，并将它们首尾相连。该技术被称为逐段贝塞尔曲线（Piecewise Bezier Curves）。

对于每段曲线，我们均使用四个控制点，即三次贝塞尔曲线。

该方法有非常广泛的应用，如Photoshop中的钢笔工具。

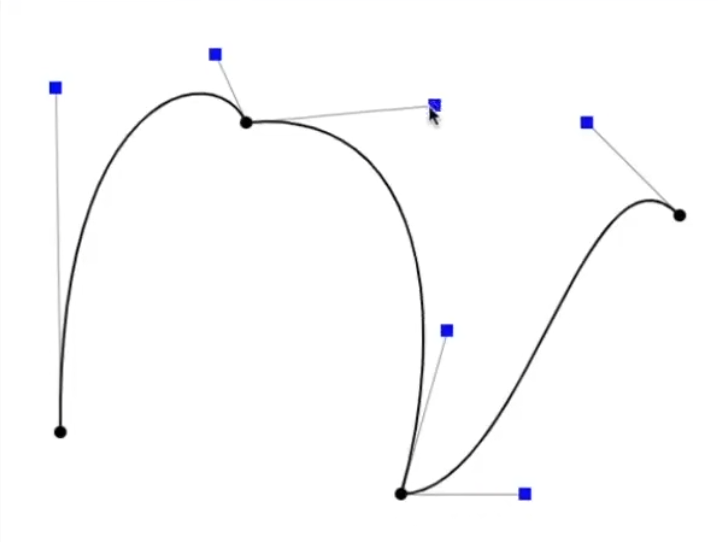
若要让过度点处的曲线光滑无转折，将两个手柄拉到共线且等距即可。

连续性

当一个曲线的终点是第二个曲线的起点时，我们称这两个曲线为C0连续（C0 Continuity）。

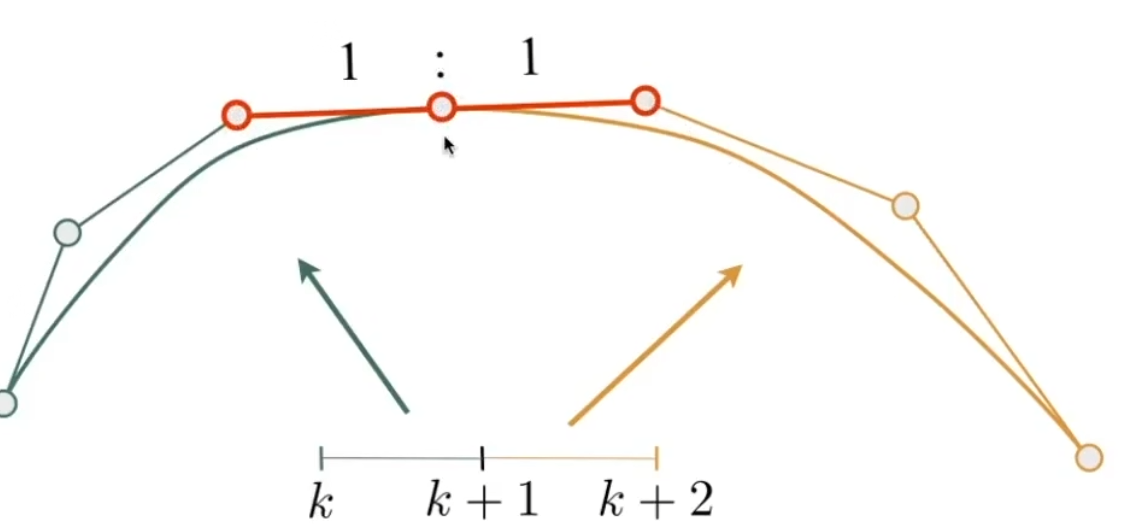
当两个曲线满足C0连续时，若连续点的两个“手柄”共线且等距，即$a_n=b_0=\frac{1}{2}(a_{n-1}+b_1)$时，我们称这两个曲线为C1连续。

a代表曲线a，a_n代表曲线a的第n个点，即终点；b代表曲线b，b_0代表曲线b的起点。

样条曲线

样条曲线（Spline）是通过一组给定点生成的平滑连续曲线。曲线的形态由控制点控制。

B-样条曲线（B-Spline）比起贝塞尔曲线需要更多的信息，它可以满足更多的需求，能对曲线有更精细的控制。这类曲线具有局部性，可以知道每个控制点对曲线的影响范围。

曲面

贝塞尔曲面

贝塞尔曲面（Bezier Surface）是对二维空间中两个方向分别应用贝塞尔曲线，然后进行双线性插值得到的。

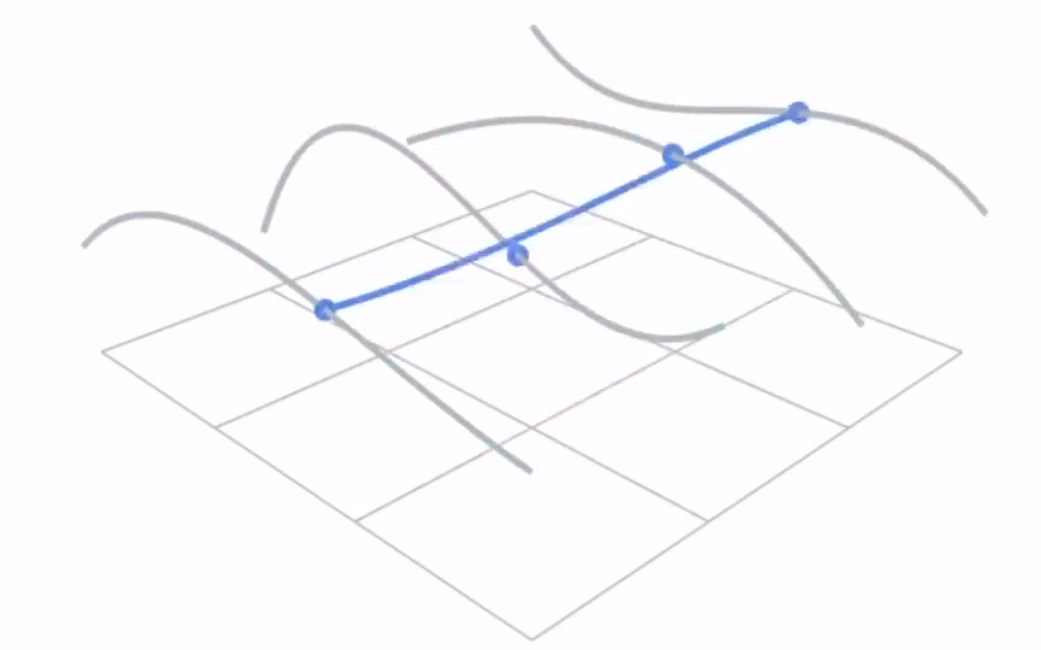
如图，我们首先定义四个横向贝塞尔曲线，然后标记处四个曲线上相同横坐标的点，将它们作为纵向贝塞尔曲线的四个控制点，这样就绘制出了一条纵向曲线。在横坐标不断变化的过程中，这条曲线会扫描出一个面，这个面就是贝塞尔曲面。

网格

对于网格（Mesh），一般存在细分（Subdivision）、简化（Simplification）、规范化（Regularization）三种操作。

细分

细分操作用于增加三角形数量，使得曲面更加光滑，表面有更多细节。

细分分为两步：首先将一个三角形分出更多小三角形，然后移动顶点位置，使模型更光滑。

Loop细分

最简单的细分操作为Loop细分。该方法仅适用于三角形网格。将三角形三条边的中点相连接，即可得到四个小三角形。对于新顶点（原先的中点）和老顶点，有不同的规则进行顶点位置的改变：

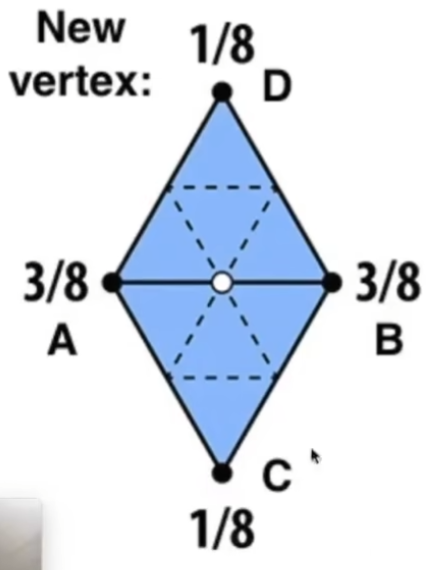
如图，对于新顶点，它一般情况下位于一条边上并且被若干小三角形共享。我们把同时含有新旧顶点的小三角形的旧顶点称为A、B，否则称为C、D，则新顶点的位置应当被更新为3/8*(A+B)+1/8*(C+D)。

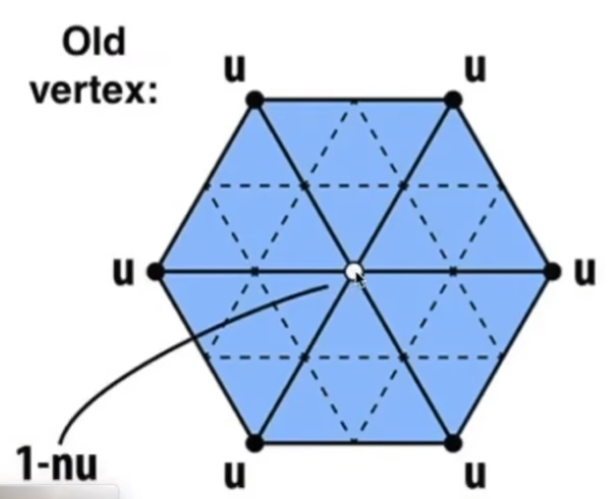
对于旧顶点，一部分位置不变，另一部分按以下规则变化：

一个顶点所连接的边的数量被称为顶点的度（Degree），记为n。定义数量u，当n=3时，u=3/16；其他情况下，u=3/(8n)。则旧顶点的位置更新为：(1-n*u)*原位置+u*相邻顶点位置和。

Catmull-Clark细分

Catmull-Clark细分适用于任意形状的网格。

首先定义，在网格中存在两类面：四边形面（Quad Face）和非四边形面（Non-Quad Face）。其次，定义度不为4的点均为奇异点（Extraordinary Vertex）。

对于每个边，我们取其中点；对于每个面内部我们同样取一个点（可以是重心），然后将边上中点和面上的点相连，完成新顶点的生成：

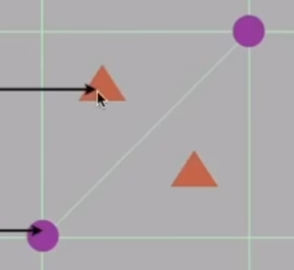
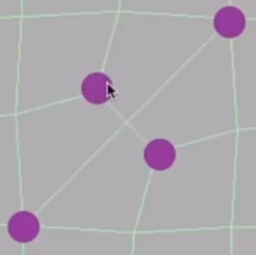
随后，我们可以发现，只要是在非四边形面内取的点，在连接后均为奇异点（因为它要和非四边形的每条边相连，度必定不为4）。并且，在完成连接后，新增了（原本非四边形面个数）个奇异点，且目前已经不存在非四边形面了。我们可以认为，该过程将非四边形面规范化为四边形面的同时，总会引入一个奇异点。

我们可以总结：第一次Catmull-Clark细分会将所有非四边形面转换为四边形面。在之后的细分步骤中，奇异点数不会增加。

接下来进入更新顶点位置步骤：

首先考虑新取的点——

对于四边形面内取的点，其新位置为：$f=\frac{v_1+v_2+v_3+v_4}{4}$

对于四边形边上取的点，其新位置为：$e=\frac{v_1+v_2+f_1+f_2}{4}$

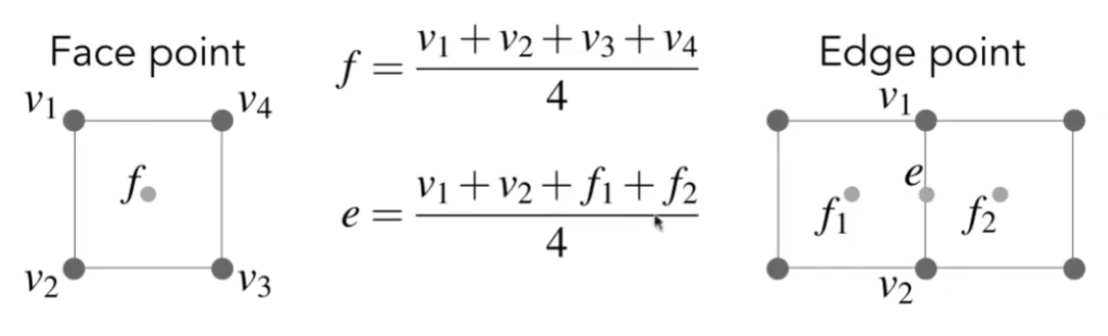
对于旧顶点，其新位置为：$v=\frac{f_1+f_2+f_3+f_4+2(m_1+m_2+m_3+m_4)+4p}{16}$

简化

简化操作用于在保持原有形态不变的情况下减少三角形数量，优化渲染性能。

边坍缩（Edge Collapsing）法：找到一条边，将边的两个顶点合并为一个顶点。

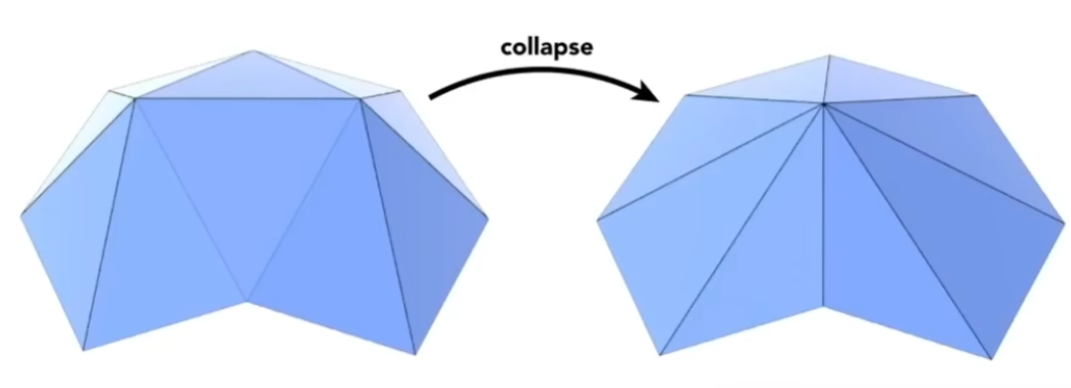
实际应用中，寻找需要坍缩的边比较困难。我们引入二次误差度量（Quadric Error Metrics）：

二次误差指：我们需要找到一个新顶点，使新顶点到原本的与新顶点关联的若干个面的距离的平方和最小。

结合边坍缩算法，在实际的简化操作中，程序将遍历每一条边，计算每一条边坍缩后的二次误差并记录。在实际坍缩时，从二次误差最小的边开始。

一个问题是，一个边坍缩后会引起其他边的变化，变化的边的二次误差需要重新计算。因此，需要一种数据结构，它既能快速地取到最小值，又能快速地以小代价更新元素。优先队列（堆）便具有这种特性。

规范化

规范化操作用于使网格中的三角形形状趋于一致，更加均匀。